Giúp tớ với:
a) \(\left|0,5.x-2\right|-\left|x+\dfrac{2}{3}\right|=0\)
b) \(2x-\left|x+1\right|=\dfrac{1}{4}\)
c) \(3x-\left|x+15\right|=\dfrac{5}{4}\)
d) \(\dfrac{3}{2}-\left|\dfrac{5}{4}+3x\right|=\dfrac{1}{4}\)
e) \(\left|4x-1\right|=\left|3x-\dfrac{1}{2}\right|\)
f) \(\left|2x-1\right|=\left|x+\dfrac{1}{3}\right|\)

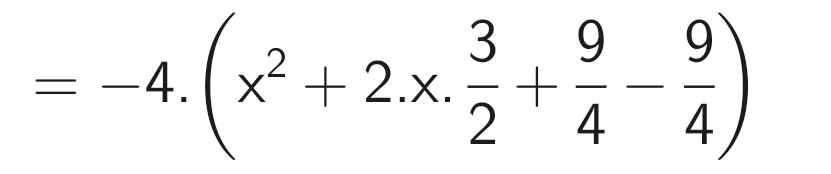
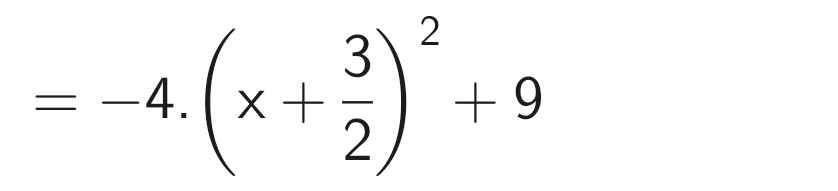
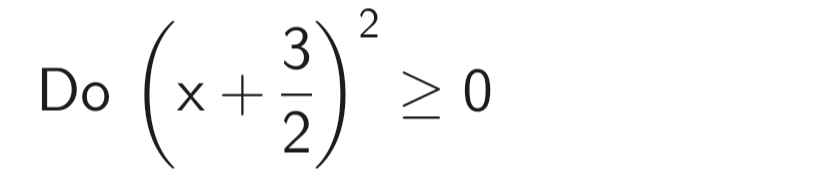
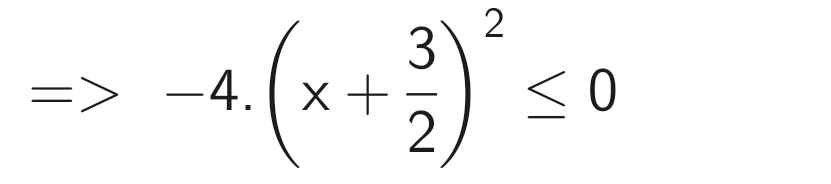
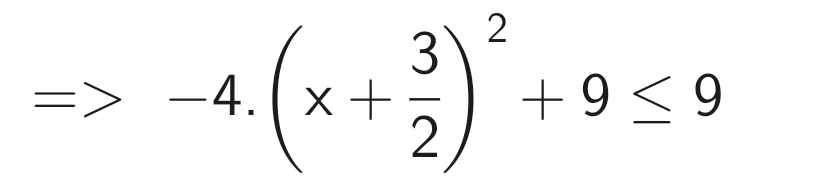
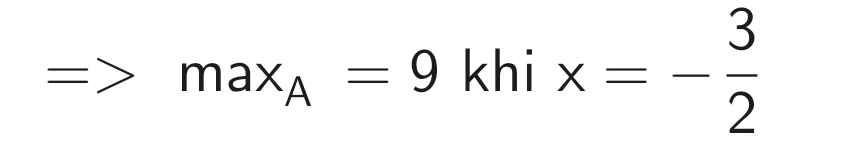
a: \(\left|0,5x-2\right|-\left|x+\dfrac{2}{3}\right|=0\)
=>\(\left|\dfrac{1}{2}x-2\right|=\left|x+\dfrac{2}{3}\right|\)
=>\(\left[{}\begin{matrix}\dfrac{1}{2}x-2=x+\dfrac{2}{3}\\\dfrac{1}{2}x-2=-x-\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{2}x=2+\dfrac{2}{3}=\dfrac{8}{3}\\\dfrac{3}{2}x=-\dfrac{2}{3}+2=\dfrac{4}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{8}{3}:\dfrac{-1}{2}=\dfrac{8}{3}\cdot\left(-2\right)=-\dfrac{16}{3}\\x=\dfrac{4}{3}:\dfrac{3}{2}=\dfrac{8}{9}\end{matrix}\right.\)
b:
\(2x-\left|x+1\right|=\dfrac{1}{4}\)
=>\(\left|x+1\right|=2x-\dfrac{1}{4}\)
=>\(\left\{{}\begin{matrix}2x-\dfrac{1}{4}>=0\\\left(2x-\dfrac{1}{4}\right)^2=\left(x+1\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{8}\\\left(2x-\dfrac{1}{4}-x-1\right)\left(2x-\dfrac{1}{4}+x+1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{8}\\\left(x-\dfrac{5}{4}\right)\left(3x+\dfrac{3}{4}\right)=0\end{matrix}\right.\Leftrightarrow x=\dfrac{5}{4}\)
c: \(3x-\left|x+15\right|=\dfrac{5}{4}\)
=>\(\left|x+15\right|=3x-\dfrac{5}{4}\)
=>\(\left\{{}\begin{matrix}3x-\dfrac{5}{4}>=0\\\left(3x-\dfrac{5}{4}\right)^2=\left(x+15\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{5}{12}\\\left(3x-\dfrac{5}{4}-x-15\right)\left(3x-\dfrac{5}{4}+x+15\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{5}{12}\\\left(2x-16,25\right)\left(4x+\dfrac{55}{4}\right)=0\end{matrix}\right.\Leftrightarrow x=8,125\)
d: \(\dfrac{3}{2}-\left|\dfrac{5}{4}+3x\right|=\dfrac{1}{4}\)
=>\(\left|3x+\dfrac{5}{4}\right|=\dfrac{3}{2}-\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(\left[{}\begin{matrix}3x+\dfrac{5}{4}=\dfrac{5}{4}\\3x+\dfrac{5}{4}=-\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=0\\3x=-\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{6}\end{matrix}\right.\)
e: \(\left|4x-1\right|=\left|3x-\dfrac{1}{2}\right|\)
=>\(\left[{}\begin{matrix}4x-1=3x-\dfrac{1}{2}\\4x-1=-3x+\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x-3x=-\dfrac{1}{2}+1\\4x+3x=\dfrac{1}{2}+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\7x=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{14}\end{matrix}\right.\)
f: \(\left|2x-1\right|=\left|x+\dfrac{1}{3}\right|\)
=>\(\left[{}\begin{matrix}2x-1=x+\dfrac{1}{3}\\2x-1=-x-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=\dfrac{1}{3}+1\\2x+x=-\dfrac{1}{3}+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{4}{3}\\3x=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=\dfrac{2}{9}\end{matrix}\right.\)