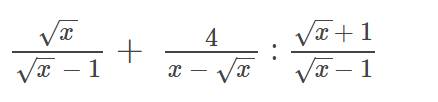\(\dfrac{2x+4}{4}-\dfrac{2x-7}{5}=\dfrac{2x-13}{6}\)

\(15\left(2x+4\right)-12\left(2x-7\right)=10\left(2x-13\right)\)
\(30x+60-24x+84=20x-130\)

\(30x-24x-20x=-130-60-84\)

\(-14x=-274\)

\(x=\dfrac{137}{7}\approx19,\left(571428\right)\)

\(\dfrac{\sqrt{x}}{\sqrt{x}-1}\)+\(\dfrac{4}{\sqrt{x}\left(\sqrt{x}-1\right)}\)x\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

=\(\dfrac{\sqrt{x}}{\sqrt{x}-1}\)+​​\(\dfrac{4}{\sqrt{x}\left(\sqrt{x}+1\right)}\)​​

=\(\dfrac{\sqrt{x}\cdot\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)+\(\dfrac{4\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

=\(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)+\(\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

=\(\dfrac{x+4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

Còn lại tự làm đê :))) công nhận ai ra đề mà ác vc

giải giúp tui!!Please!!

Cai nay lop 7 ma, Ap dung cong thuc tinh canh huyen tam giac vuong la ra duong cheo cua cac tam giac trong hinh thang

\(x^2\sqrt{9-x^2}\)

Ta có:

\(9-x^2\le9\forall x\)

\(Minx^2\sqrt{9-x^2}=0\Leftrightarrow x=0\)