Có bao nhiêu cách xếp 5 người ngồi trên ghế dài sao cho hai người nhiều tuổi nhất ngồi cạnh nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
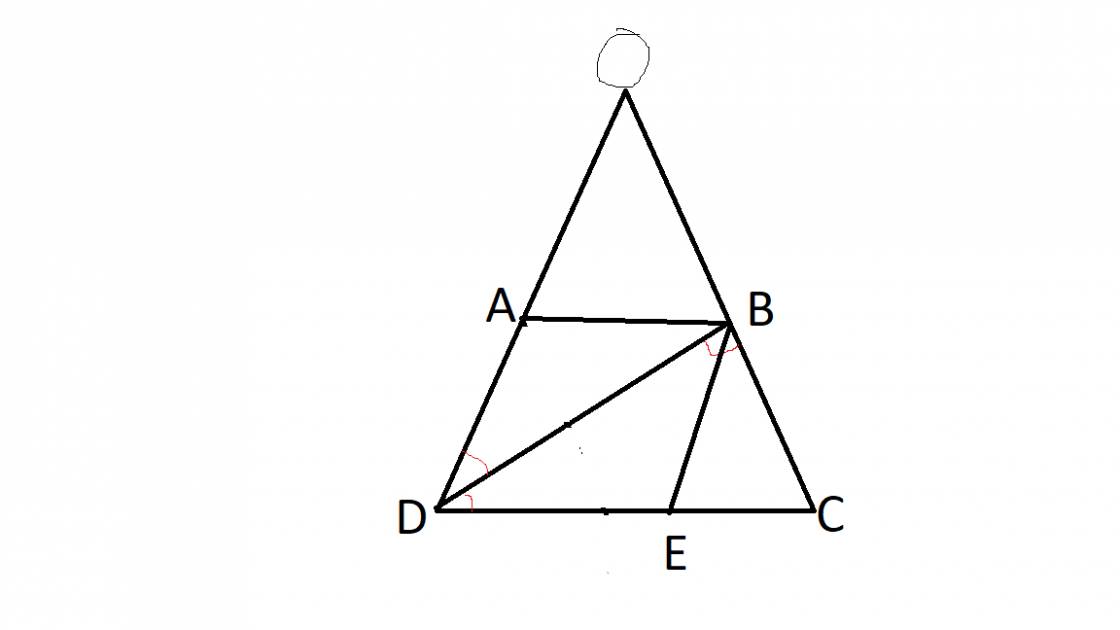
Ta có: AD=BC=3cm (t/c hthang)
Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)
Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)
=>∠ABD=∠BDC
=>∆ABD cân tại A
=>AD=BC=3cm
Vì ∆DBC vuông tại B
nên ∠BDC+∠C=90o
Mà ∠ADC=∠C (do ABCD là hình thang cân)
và ∠BDC=1/2 ∠ADC
=> ∠BCD=1/2∠C
Khi đó: ∠C+1/2∠C=90o=>∠C=60o
- Kẻ từ B 1 đường thẳng // AD cắt CD tại E
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
Mà ∠BEC=∠ADC(đồng vị)
=>∠BEC=∠C
=>∆BEC cân tại B có ∠C=60o
=>∆BEC là ∆ cả cân cả đều
=> EC=BC=3cm
Ta có: CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
Bài 2:
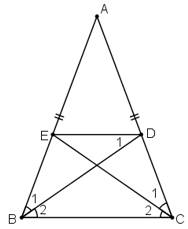
Ta có: ∆ABC là ∆ cân tại A(gt)
=>∠ABC=∠ACB
+Ta có BD là tia pgiac của ∠ABC
=>∠B1=∠B2=1/2∠ABC
+Ta có CE là tia pgiac ∠ACB
=>C1=C2=1/2∠ACB
Xét ∆
AEC và ΔADB có:
+∠A chung
+AB=AC
+C1=B1
=> ΔAEC = ΔADB
=> AE = AD
=>BCDE là hình thang cân
b) Ta có ∠ACB=∠ABC=50o(do BCDE là hình thang cân)
Ta có: ED//BC
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)
Mà ∠DEB=∠EDC
Ta có:
+∠DEB+∠AED=180o (kề bù)
=>50o+∠AED=180o
=>∠AED=180o-50o=130o
=>∠AED=∠ADE=130o

Để giải phương trình, chúng ta có thể bắt đầu bằng cách rút gọn vế trái:
x(x+2018) - 2x + 4036 = 0
Khai triển số hạng thứ nhất:
x^2 + 2018x - 2x + 4036 = 0
Kết hợp các điều khoản như:
x^2 + 2016x + 4036 = 0
Bây giờ, chúng ta có thể giải phương trình bậc hai này bằng cách chia thành thừa số hoặc sử dụng công thức bậc hai. Tuy nhiên, phương trình này không dễ dàng phân tích thành nhân tử, vì vậy chúng ta sẽ sử dụng công thức bậc hai:
x = (-b ± √(b^2 - 4ac)) / (2a)
Trong trường hợp này, a = 1, b = 2016 và c = 4036. Thay các giá trị này vào công thức bậc hai:
x = (-2016 ± √(2016^2 - 4(1)(4036))) / (2(1))
Đơn giản hóa:
x = (-2016 ± √(4064256 - 16144))/2
x = (-2016 ± √4048112)/2
x = (-2016 ± 2011,97)/2
Bây giờ, chúng ta có thể giải tìm x bằng cách sử dụng cả căn bậc hai dương và âm:
x = (-2016 + 2011,97)/2
x = (-4,03)/2
x = -2,015
x = (-2016 - 2011,97)/2
x = (-4027,97)/2
x = -2013,985
Do đó, các nghiệm của phương trình x(x+2018) - 2x + 4036 = 0 là x = -2,015 và x = -2013,985.

Bài 3:
P = \(\dfrac{1^2}{2^2-1}\). \(\dfrac{3^2}{4^2-1}\).\(\dfrac{5^2}{6^2-1}\).....\(\dfrac{2023^2}{2024^2-1}\)
P = \(\dfrac{1}{\left(2-1\right).\left(2+1\right)}\).\(\dfrac{3^2}{\left(4-1\right).\left(4+1\right)}\)....\(\dfrac{2023^2}{\left(2024-1\right).\left(2024+1\right)}\)
P = \(\dfrac{1}{1.3}\).\(\dfrac{3^2}{3.5}\).\(\dfrac{5^2}{5.7}\).\(\dfrac{7^2}{7.9}\)......\(\dfrac{2021^2}{2021.2023}\).\(\dfrac{2023^2}{2023.2025}\)
P = \(\dfrac{1}{2025}\)

\(...P=x^2-8x+16+x^2+2xy+y^2+2y^2-2y+2\)
\(P=\left(x-4\right)^2+\left(x+y\right)^2+2\left(y^2-y+1\right)\left(1\right)\)
Xét \(y^2-y+1=y^2-y+\dfrac{1}{4}-\dfrac{1}{4}+1=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\left(\left(y-\dfrac{1}{2}\right)^2\ge0\right)\)
\(\Rightarrow2\left(y^2-y+1\right)\ge2.\dfrac{3}{4}=\dfrac{3}{2}\)
mà \(\left(x-4\right)^2\ge0;\left(x+y\right)^2\ge0\)
\(\left(1\right)\Rightarrow P\ge\dfrac{3}{2}\Rightarrow Min\left(P\right)=\dfrac{3}{2}\)

E = 16\(x^2\) + 5 + 8\(x\) - 4y + y2
E = (16\(x^2\) + 8\(x\) + 1) + (y2 - 4y + 4)
E = (4\(x\) + 1)2 + (y - 2)2
Vì (4\(x\) + 1)2 ≥ 0
(y - 2)2 ≥ 0
Cộng vế với vế ta có: (4\(x\) + 1)2 + (y -2)2 ≥ 0
Vậy Emin = 0 ⇔ \(\left\{{}\begin{matrix}4x+1=0\\y-2=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=-\dfrac{1}{4}\\y=2\end{matrix}\right.\)
Kết luận giá trị nhỏ nhất của E là: 0 xảy ra khi \(x\) = -\(\dfrac{1}{4}\); y =2

Để xác định các hệ số a, b, c, ta cần giải phương trình sau: (a + by + cy^2)(y + 3) = y^3 + 2y^2 - 3y Mở ngoặc và sắp xếp các thành phần theo bậc của y, ta có: ay^3 + (3a + by^2) + (3b + cy)y + 3c = y^3 + 2y^2 - 3y So sánh các hệ số của các bậc của y, ta có hệ phương trình sau: a = 1 3a + b = 2 3b + c = -3 3c = 0 Từ hệ phương trình trên, ta có: a = 1 b = 2 - 3a = 2 - 3(1) = -1 c = -3 - 3b = -3 - 3(-1) = 0 Vậy, các hệ số a, b, c là: a = 1, b = -1, c = 0.

Để tìm thời điểm mà kim giờ và kim phút tạo với nhau góc 120 độ, ta cần xác định thời điểm nào trong khoảng từ 12 giờ đến 1 giờ mà góc giữa kim giờ và kim phút là 120 độ. Góc giữa kim giờ và kim phút được tính bằng công thức sau: Góc = |30h - 11m/2| Trong đó: - h là giờ - m là phút Ta có thể thử từng thời điểm trong khoảng từ 12 giờ đến 1 giờ để tìm thời điểm thích hợp. Ví dụ: - Thử với 12 giờ: Góc = |30*12 - 11*0/2| = |360 - 0/2| = |360| = 360 (không thỏa mãn) - Thử với 12 giờ 15 phút: Góc = |30*12 - 11*15/2| = |360 - 165/2| = |360 - 82.5| = |277.5| = 277.5 (không thỏa mãn) - Thử với 12 giờ 30 phút: Góc = |30*12 - 11*30/2| = |360 - 165| = |195| = 195 (không thỏa mãn) - Thử với 12 giờ 45 phút: Góc = |30*12 - 11*45/2| = |360 - 247.5| = |112.5| = 112.5 (không thỏa mãn) - Thử với 1 giờ: Góc = |30*1 - 11*0/2| = |30 - 0/2| = |30| = 30 (không thỏa mãn) Vậy không có thời điểm nào trong khoảng từ 12 giờ đến 1 giờ mà kim giờ và kim phút tạo với nhau góc 120 độ.
Để tìm thời điểm mà kim giờ và kim phút tạo với nhau góc 120 độ, ta cần xác định thời điểm nào trong khoảng từ 12 giờ đến 1 giờ mà góc giữa kim giờ và kim phút là 120 độ. Góc giữa kim giờ và kim phút được tính bằng công thức sau: Góc = |30h - 11m/2| Trong đó: - h là giờ - m là phút Ta có thể thử từng thời điểm trong khoảng từ 12 giờ đến 1 giờ để tìm thời điểm thích hợp. Ví dụ: - Thử với 12 giờ: Góc = |30*12 - 11*0/2| = |360 - 0/2| = |360| = 360 (không thỏa mãn) - Thử với 12 giờ 15 phút: Góc = |30*12 - 11*15/2| = |360 - 165/2| = |360 - 82.5| = |277.5| = 277.5 (không thỏa mãn) - Thử với 12 giờ 30 phút: Góc = |30*12 - 11*30/2| = |360 - 165| = |195| = 195 (không thỏa mãn) - Thử với 12 giờ 45 phút: Góc = |30*12 - 11*45/2| = |360 - 247.5| = |112.5| = 112.5 (không thỏa mãn) - Thử với 1 giờ: Góc = |30*1 - 11*0/2| = |30 - 0/2| = |30| = 30 (không thỏa mãn) Vậy không có thời điểm nào trong khoảng từ 12 giờ đến 1 giờ mà kim giờ và kim phút tạo với nhau góc 120 độ.
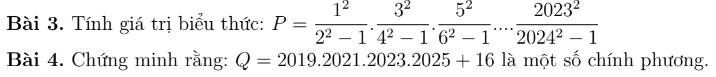

Mình đag cần gấp. Giúp mik vs
Để xếp hạng hai người nhiều tuổi nhất ngồi cạnh nhau, ta có thể xem hai người này như một vị trí. Do đó ta có 4 đơn vị để xếp trên ghế dài.
Số cách sắp xếp 4 đơn vị trên ghế dài là 4! = 4 x 3 x 2 x 1 = 24.
Tuy nhiên, hai người nhiều tuổi nhất có thể ngồi bên trái hoặc bên phải của nhau, nên số cách xếp hạng 5 người trên ghế dài sao cho hai người nhiều tuổi nhất ngồi cạnh nhau là 24 x 2 = 48.