cho tam giác ABC .Vẽ các đường phân giác BD và Ce.Gọi P,N lần lượt là hình chiếu của A trên BD và CE.Gọi M và Q lần lượt là hình chiếu của A trên đường phân giác ngoài tại B và C.cm M,N,Q thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(=\dfrac{\sqrt{a}\left(\sqrt{ab}+1\right)-\sqrt{b}\left(\sqrt{ab}+1\right)}{\left(\sqrt{ab}-1\right)\left(\sqrt{ab}+1\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{ab}+1\right)}{\left(\sqrt{ab}-1\right)\left(\sqrt{ab}+1\right)}\)
\(=\dfrac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}-1}\)

Lời giải:
a. Áp dụng định lý về hệ thức lượng trong tam giác vuông cho tam giác $ABH$ có:
$AD.AB=AH^2(1)$
Tương tự với tam giác $AHC$: $AE.AC=AH^2(2)$
Từ $(1); (2)\Rightarrow AD.AB=AE.AC$
$\Rightarrow \frac{AD}{AE}=\frac{AC}{AB}$
-------------------
ĐPCM $\Leftrightarrow \frac{BD^2}{BC^2}=\frac{BH^3}{BC^3}$
$\Leftrightarrow BD^2.BC=BH^3(*)$
Thật vậy:
Do $DH\parallel AC$ nên $\frac{BD}{BA}=\frac{BH}{BC}$
$\Rightarrow BD.BC=BH.BA$
$\Rightarrow BD^2.BC=\frac{BH^2.BA^2}{BC}=\frac{BH^2.BH.BC}{BC}$ (theo hệ thức lượng trong tgv)
$=BH^3$
$(*)$ được chứng minh
Áp dụng hệ thức lượng trong tam giác vuông BDH với đường cao HD:
\(BH^2=BD.AB\)
Xét hai tam giác vuông BDH và BAC có \(\widehat{B}\) chung
\(\Rightarrow\Delta_VBDH\sim\Delta_VBAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{AB}=\dfrac{BH}{BC}\Rightarrow BD=\dfrac{BH.AB}{BC}\)
\(\Rightarrow BD^2=\dfrac{BH.BD.AB}{BC}=\dfrac{BH^3}{BC}\)
\(\Rightarrow\dfrac{BD^2}{BC^2}=\dfrac{BH^3}{BC^3}\)
\(\Rightarrow\sqrt[3]{\dfrac{BD^2}{BC^2}}=\dfrac{BH}{BC}\) (đpcm)

Lời giải:
Gọi bt cần tính là $A$
\(\sqrt{\frac{2-\sqrt{3}}{2+\sqrt{3}}}=\sqrt{\frac{(2-\sqrt{3})^2}{(2+\sqrt{3})(2-\sqrt{3})}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)
\(\frac{2+\sqrt{3}}{2-\sqrt{3}}=\frac{(2+\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}=(2+\sqrt{3})^2=7+4\sqrt{3}\)
Khi đó: $A=\sqrt{7+4\sqrt{3}+2-\sqrt{3}}=\sqrt{9+3\sqrt{3}}$
22-( \(\sqrt{ }\)3 )2= 1
4+3+4\(\sqrt{ }\)3 + 4+3- 4\(\sqrt{ }\)3 = \(\sqrt{ }\)14
đáp số \(\sqrt{ }\)14
?

Cho tam giác abc có ah là đường cao, bm là truyen tuyến cắt ah tại g. ah =5cm. Tính diện tích tam giác abc

Xét tam giác ABC đều , đường cao AH
=> AH đồng thời là đường trung tuyế
=> HB = BC/2 = 8 cm
Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-BH^2}=8\sqrt{3}\)cm

- Hạ \(BE\perp CD\) tại E.
- Tứ giác ABED có: \(\widehat{DAB}=\widehat{ADE}=\widehat{BED}=90^0\)
\(\Rightarrow\)ABED là hình chữ nhật.
\(\Rightarrow AB=DE=6\left(cm\right);AD=BE=3\left(cm\right)\)
\(\Rightarrow CE=CD-DE=8-6=2\left(cm\right)\)
- \(\Delta BCE\) vuông tại E có: \(BC^2=BE^2+CE^2\)
\(\Rightarrow BC=\sqrt{BE^2+CE^2}=\sqrt{3^2+2^2}=\sqrt{13}\left(cm\right)\)
\(\tan\widehat{CBE}=\dfrac{CE}{BE}=\dfrac{2}{3}\Rightarrow\widehat{CBE}\approx33^0\)
\(\Rightarrow\widehat{ABC}=\widehat{ABE}+\widehat{CBE}\approx90^0+33^0=123^0\)
\(\tan\widehat{BCD}=\dfrac{BE}{CE}=\dfrac{3}{2}\Rightarrow\widehat{BCD}\approx56^0\)
Phương Anh, toán phân biệt chữ cái, chữ nhỏ. Bạn xem lại bài, viết giống như bài hỏi nhé.
A, B ...điểm
góc A, góc B
AB, BC ...cạnh
AB= 6 cm ...độ dài cạnh

khỏi chứng minh
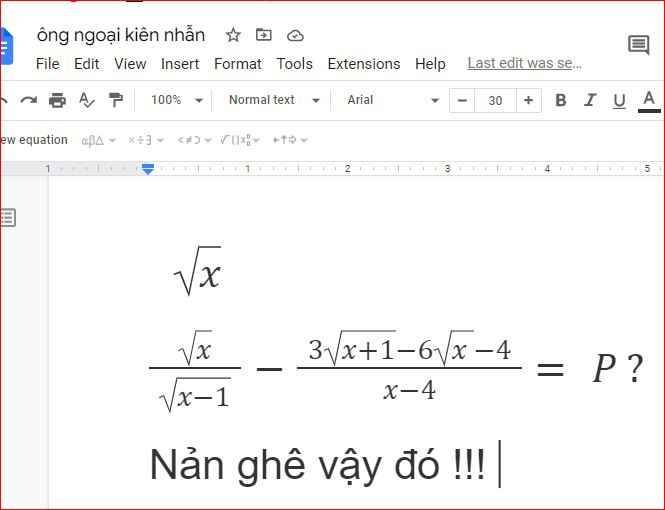
căn có cả dấu = nằm bên trong , mà còn dấu - của 4 , = - 4 ???
viết lại câu hỏi nhé !

- Sửa đề: CMR: M,N,P,Q thẳng hàng.
* AM, AN, AP, AQ cắt BC lần lượt tại F,G,H,I.
- \(\Delta AMB\) và \(\Delta FMB\) có: \(\widehat{AMB}=\widehat{FMB}=90^0;\widehat{ABM}=\widehat{FBM};BM\) là cạnh chung.
\(\Rightarrow\Delta AMB=\Delta FMB\left(g-c-g\right)\)
\(\Rightarrow MA=MF\) nên \(M\) là trung điêm AF.
- Tương tự: N là trung điểm AG, P là trung điểm AH, Q là trung điểm AI.
\(\Rightarrow MN,NP,PQ\) lần lượt là đường trung bình của \(\Delta AFG,\Delta AGH,\Delta AHI\)
\(\Rightarrow MN\)//NP//PQ//BC.
\(\Rightarrow\)M,N,P,Q thẳng hàng.