
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(x-2\right)^2+2x+1\)
\(=\left(x^2-2\times x\times2+2^2\right)+2x+1\)
\(=\left(x^2-4x+4\right)+2x-1\)
\(=x^2-4x+4+2x-1\)
\(=x^2-2x+3\)

a) Ta có:
\(x^2-x+1\)
\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\) và \(\dfrac{3}{4}>0\) nên
\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
\(\Rightarrow x^2-x+1>0\forall x\)

1.
$3x^4-48=3(x^4-16)=3[(x^2)^2-4^2]=3(x^2-4)(x^2+4)$
$=3(x-2)(x+2)(x^2+4)$
2.
$x^3-4x^2+8x-8=(x^3-8)-(4x^2-8x)$
$=(x-2)(x^2+2x+4)-4x(x-2)=(x-2)(x^2+2x+4-4x)=(x-2)(x^2-2x+4)$
3.
$x^4-27x=x(x^3-27)=x(x^3-3^3)=x(x-3)(x^2+3x+9)$
4.
$x^4-x^3+x^2-1=(x^4-x^3)+(x^2-1)=x^3(x-1)+(x-1)(x+1)$
$=(x-1)(x^3+x+1)$
5.
$x^5+x^3-x^2-1=(x^5+x^3)-(x^2+1)=x^3(x^2+1)-(x^2+1)$
$=(x^2+1)(x^3-1)=(x^2+1)(x-1)(x^2+x+1)$
6.
$x^3+2x^2+2x+1=(x^3+x^2)+(x^2+2x+1)=x^2(x+1)+(x+1)^2$
$=(x+1)(x^2+x+1)$
7.
$x^3+x^2-4x-4=(x^3+x^2)-(4x+4)=x^2(x+1)-4(x+1)$
$=(x+1)(x^2-4)=(x+1)(x-2)(x+2)$
8.
$x^4-2x^3+2x-1=(x^4-2x^3+x^2)-(x^2-2x+1)$
$=(x^2-x)^2-(x-1)^2=x^2(x-1)^2-(x-1)^2=(x-1)^2(x^2-1)=(x-1)^2(x-1)(x+1)$

Lời giải:
a. $A=3xy(x^2+2xy+y^2)=3xy(x+y)^2=3.\frac{1}{2}.\frac{-1}{3}(\frac{1}{2}+\frac{-1}{3})^2=\frac{-1}{72}$
b.
$B=(-1)^2.3^2+(-1).3+(-1)^3+3^3=32$
c.
$D=5^2+4.5.1-3.1^3=42$
d.
$D=2xy(x+y)=2.1(-3)(1-3)=12$
e.
$M=\frac{(x+2)(2x-1)}{x+2}=2x-1=2(-1)-1=-3$

Lời giải:
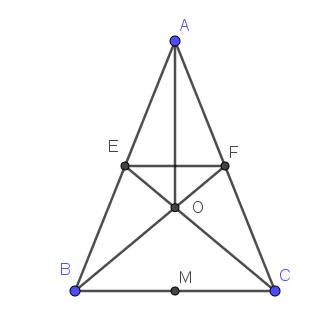
a. $E, F$ là trung điểm của $AB, AC$
$\Rightarrow EF$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow EF\parallel BC$
$\Rightarrow EFCB$ là hình thang
Mà $\widehat{B}=\widehat{C}$ (do $ABC$ cân tại $A$)
$\Rightarrow EFCB$ là hình thang cân.
b. Vì $EFCB$ là htc nên $EC=BF$
Vì $E,F$ là trung điểm $AB,AC$ và $AB=AC$ nên:
$EB=AB:2=AC:2=FC$
Xét tam giác $EBC$ và $FCB$ có:
$EB=FC$
$BC$ chung
$EC=FB$ (cmt)
$\Rightarrow \triangle EBC=\triangle FCB$ (c.c.c)
$\Rightarrow \widehat{ECB}=\widehat{FBC}$
Hay $\widehat{OCB}=\widehat{OBC}$
$\Rightarrow OBC$ là tam giác cân.
c. Xét tam giác $AOB$ và $AOC$ có:
$AO$ chung
$AB=AC$
$OB=OC$ (do tam giác $OBC$ cân tại $O$)
$\Rightarrow \triangle AOB=\triangle AOC$ (c.c.c)
$\Rightarrow \widehat{BAO}=\widehat{CAO}$
$\Rightarrow AO$ là phân giác $\widehat{A} (1)$
Mặt khác: Tam giác $ABC$ cân tại $A$ nên trung tuyến AM đồng thời là phân giác $AM$ của góc $\widehat{A}(2)$
Từ $(1), (2)\Rightarrow A,O,M$ thẳng hàng.

\(2a^2+8b^2-8ab\)
\(=2\left(a^2-4ab+4b^2\right)\)
\(=2\left(a-2b\right)^2\)
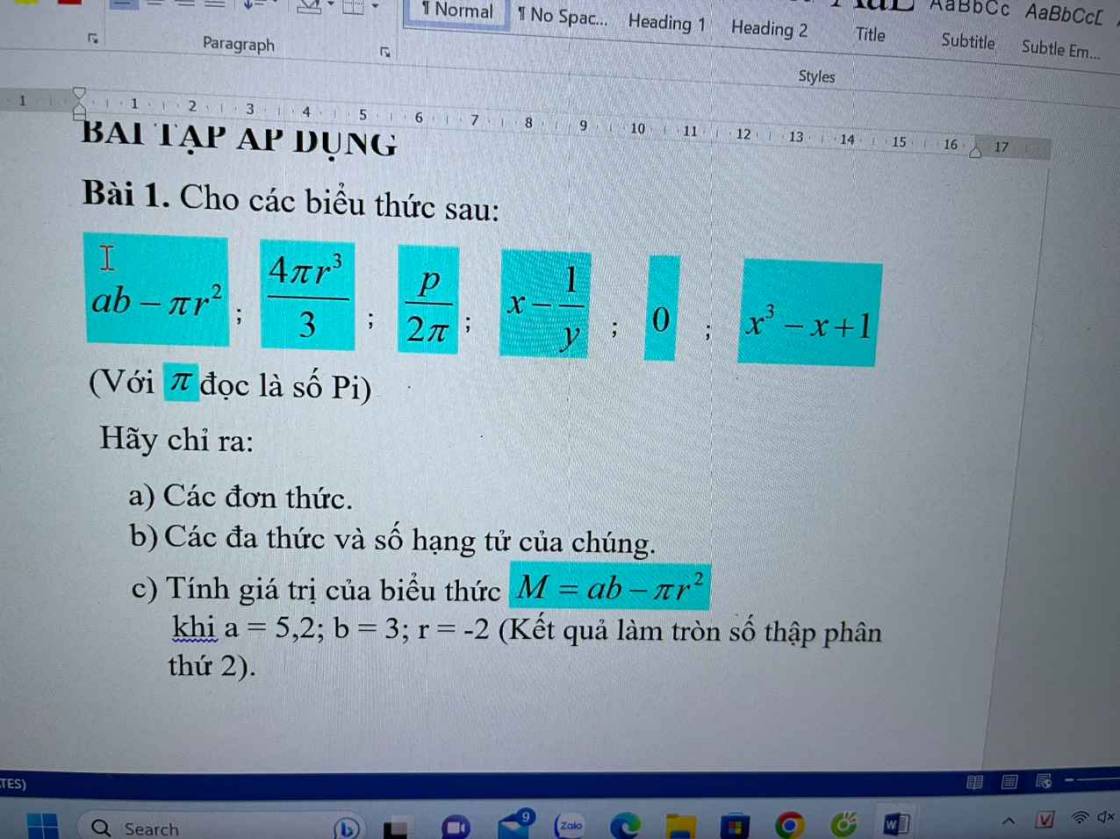
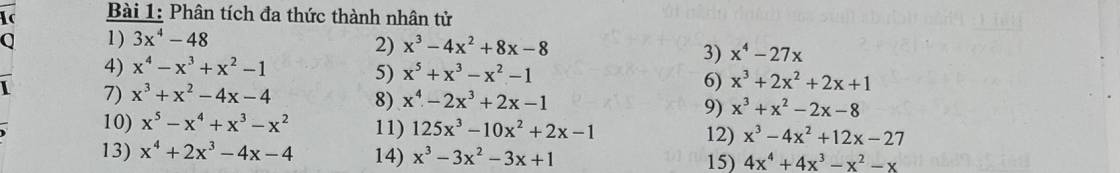
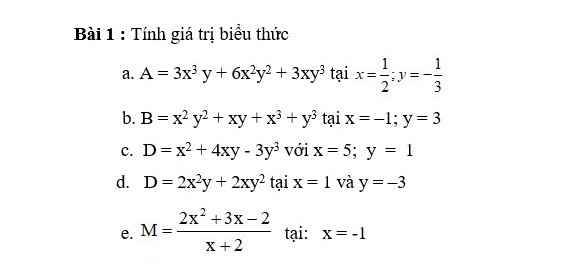

`@` `\text {Ans}`
`\downarrow`
`2,`
`a)`
`-5x^2y^4z^5 (-3xyz^2)`
`= (-5).(-3) . (x^2 . x) . (y^4 . y) . (z^5 . z^2)`
`= 15 x^3 y^5 z^7`
Hệ số: `15`
Phần biến: `x^3 y^5 z^7`
Bậc: `3 + 5 + 7 = 15`
`b)`
`12xy^3z^5 .`\((\dfrac{1}{4}x^3z^3)\)
`=`\((12. \dfrac{1}{4})\)`. (x . x^3) . y^3 . (z^5 . z^3)`
`= 3 x^4 y^3 z^8`
Hệ số: `3`
Phần biến: `x^4y^3z^8`
Bậc: `4+3+8 = 15`
`c)`
\(x^3 . (\dfrac{-5}{4}x^2y)(\dfrac{2}{5}x^3y^4)\)
`=`\(\left(-\dfrac{5}{4}\cdot\dfrac{2}{5}\right)\left(x^3\cdot x^2\cdot x^3\right)\left(y\cdot y^4\right)\)
`=`\(-\dfrac{1}{2}x^8y^5\)
Hệ số: \(-\dfrac{1}{2}\)
Phần biến: `x^8y^5`
Bậc: `8 + 5 = 13`