a: \(M\in SA\)

=>\(M\in\left(DMN\right)\cap\left(SAD\right)\)

mà \(D\in\left(DMN\right)\cap\left(SAD\right)\)

nên \(\left(DMN\right)\cap\left(SAD\right)=MD\)

b: \(N\in BC\)

=>\(N\in\left(DMN\right)\cap\left(ABCD\right)\)

mà \(D\in\left(DMN\right)\cap\left(ABCD\right)\)

nên \(\left(DMN\right)\cap\left(ABCD\right)=DN\)

c: \(M\in SA\)

=>\(M\in\left(DMN\right)\cap\left(SAB\right)\)

Trong mp(ABCD), gọi E là giao điểm của DN với AB

=>\(E\in\left(DMN\right)\cap\left(SAB\right)\)

Do đó: \(\left(DMN\right)\cap\left(SAB\right)=ME\)

2

• "Tuổi trẻ"của Xuân Diệu: Thể hiện khát vọng sống mãnh liệt, hăng say, yêu đời, trân trọng tuổi trẻ của con người.
• "Sống chết mặc bay"của Nguyễn Quang Sáng: Phê phán thói vô trách nhiệm, ích kỷ của tầng lớp thống trị, đồng thời đề cao tinh thần yêu nước, ý thức trách nhiệm của người nông dân.
• "Chiếc lược ngà"của Nguyễn Quang Sáng: Ca ngợi tình phụ tử thiêng liêng, bất diệt, đồng thời thể hiện niềm tin vào tương lai tươi sáng của dân tộc.
• "Lặng lẽ trên Sông Đông"của M.A. Sholokhov: Khắc họa hình ảnh những con người bình dị nhưng có ý chí phi thường, góp phần bảo vệ Tổ quốc trong chiến tranh.
• "Bài ca hi vọng" của Tố Hữu: Thể hiện niềm tin vào tương lai tươi sáng của dân tộc, khích lệ con người sống có ý chí, nghị lực, vượt qua mọi khó khăn thử thách.

Phim ảnh:

• "Đất nước đứng lên"(1972): Miêu tả quá trình gian khổ, anh dũng của nhân dân ta trong cuộc kháng chiến chống Mỹ cứu nước.
• "Em bé Hà Nội"(1948): Hình ảnh bé gái Kim Lan dũng cảm, ngoan cường trước máy bay địch đã trở thành biểu tượng cho tinh thần yêu nước của nhân dân ta.
• "Cánh đồng hoang"(1979): Phản ánh hiện thực cuộc sống của người nông dân sau chiến tranh, đồng thời khẳng định sức sống mãnh liệt và ý chí vươn lên của họ.
• "Bi, đừng sợ!"(2010): Truyền tải thông điệp về lòng dũng cảm, tinh thần lạc quan và ý chí vượt qua nghịch cảnh.
• "Hai Phượng"(2019): Thể hiện sức mạnh của người phụ nữ Việt Nam, sẵn sàng hy sinh bản thân để bảo vệ con và chống lại cái ác.

Có \(AC=AD\sqrt{2}=a\sqrt{2}\)

\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\) \(\Rightarrow\Delta SAC\) vuông tại A.

\(\Rightarrow SA=\sqrt{SC^2-AC^2}=\sqrt{\left(a\sqrt{3}\right)^2-\left(a\sqrt{2}\right)^2}=a\)

\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.S_{ABCD}.SA=\dfrac{1}{3}.AD^2.SA=\dfrac{1}{3}.a^2.a=\dfrac{a^3}{3}\)

 Số kiểu chậu khác nhau là \(\dfrac{A^5_{20}}{5}=372096\) (chọn 5 số có kể thứ tự từ 20 số và chia cho số hoán vị vòng quanh của mỗi hoán vị phân biệt)

Chiến thắng Phát xít, hay còn gọi là Chiến thắng Đồng minh trong Chiến tranh Thế giới thứ hai, mang nhiều ý nghĩa to lớn đối với nhân loại, bao gồm:

1. Giữ gìn hòa bình và an ninh thế giới:

• Chiến thắng đã chấm dứt Chiến tranh Thế giới thứ hai, cuộc chiến tranh tàn khốc nhất trong lịch sử nhân loại, gây ra hơn 60 triệu người thiệt mạng và vô số tổn thất về vật chất.
• Chiến thắng góp phần ngăn chặn sự bành trướng của chủ nghĩa phát xít, chủ nghĩa quân phiệt, bảo vệ hòa bình và an ninh thế giới.

2. Thúc đẩy tự do và dân chủ:

• Chiến thắng đã giải phóng các dân tộc khỏi ách thống trị tàn bạo của chủ nghĩa phát xít, mở đường cho sự phát triển của tự do và dân chủ trên toàn thế giới.
• Chiến thắng góp phần thúc đẩy nhân quyền và các giá trị văn minh nhân loại.

3. Tạo điều kiện cho sự phát triển kinh tế - xã hội:

• Chiến thắng đã chấm dứt chiến tranh, tạo điều kiện cho các nước trên thế giới tập trung vào việc khôi phục và phát triển kinh tế - xã hội.
• Chiến thắng thúc đẩy hợp tác quốc tế và tạo ra môi trường thuận lợi cho giao thương, đầu tư.

4. Bài học lịch sử quý giá:

• Chiến thắng Phát xít là bài học lịch sử quý giá cho nhân loại về hậu quả thảm khốc của chiến tranh và tầm quan trọng của hòa bình.
• Chiến thắng nhắc nhở chúng ta về trách nhiệm chung trong việc bảo vệ hòa bình, an ninh thế giới và xây dựng một thế giới tốt đẹp hơn.

Đối với Việt Nam:

• Chiến thắng Phát xít góp phần quan trọng vào sự nghiệp giải phóng dân tộc của Việt Nam.
• Chiến thắng tạo điều kiện thuận lợi cho Cách mạng tháng Tám thành công, mở ra kỷ nguyên mới cho đất nước Việt Nam.

Nhìn chung, Chiến thắng Phát xít là một sự kiện lịch sử trọng đại có ý nghĩa to lớn đối với toàn nhân loại. Chiến thắng đã mang lại hòa bình, tự do, dân chủ và thúc đẩy sự phát triển kinh tế - xã hội trên toàn thế giới.

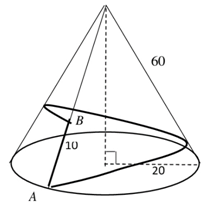
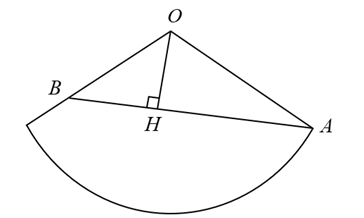
Cắt hình nón theo đường sinh OA và trải ra mặt phẳng ta đương hình quạt như hình vẽ sau

Ta có góc ở đỉnh của hình quạt là \(\dfrac{2\pi\cdot200}{600}=\dfrac{2\pi}{3}\)

Lại có, con đường từ A đến B ngắn nhất => AB là đoạn thẳng

Từ đó, đỉnh dốc H cao nhất nên gần đỉnh O => H là hình chiếu vuông góc của O lên AB

Áp dụng định lý cosin trong tam giác OAB ta có:

\(AB=\sqrt{OA^2+OB^2-2OA.OB.cos\left(\dfrac{2\pi}{3}\right)}=10\sqrt{91}\)

\(cosOBA=\dfrac{OB^2+BA^2-OA^2}{2\cdot OB\cdot OA}\)

\(HB=OB.cosOBH=OB.\left(\dfrac{OB^2+BA^2-ÓA^2}{2\cdot OA\cdot OB}\right)=\dfrac{400}{\sqrt{91}}\)Vậy quãng đường xuống dốc là \(HB=\dfrac{400}{\sqrt{91}}\)

\(I=\dfrac{E}{r+R}=0,93\) chọn D

B