a: Gọi E là giao điểm của CO và BD

Xét ΔOAC vuông tại A và ΔOBE vuông tại B có

OA=OB

\(\widehat{AOC}=\widehat{BOE}\)(hai góc đối đỉnh)

Do đó: ΔOAC=ΔOBE

=>OC=OE

Xét ΔODC vuông tại O và ΔODE vuông tại O có

OD chung

OC=OE

Do đó: ΔODC=ΔODE

ΔOAC=ΔOBE

=>\(\widehat{OCA}=\widehat{OEB}\)

mà \(\widehat{OEB}=\widehat{OCD}\)(ΔODE=ΔODC)

nên \(\widehat{OCA}=\widehat{OCD}\)

=>CO là phân giác của góc ACD

Xét ΔOAC vuông tại A và ΔOHC vuông tại H có

CO chung

\(\widehat{ACO}=\widehat{HCO}\)

Do đó: ΔOAC=ΔOHC

=>OA=OH

=>OH=AB/2

Vì OH=OA=OB=AB/2

nên H nằm trên đường tròn tâm O, đường kính AB

b: Xét (O) có

OH là bán kính

CD\(\perp\)OH tại H

Do đó: CD là tiếp tuyến của (O) tại H

a: Xét tứ giác OBDA có \(\widehat{OBD}+\widehat{OAD}=90^0+90^0=180^0\)

nên OBDA là tứ giác nội tiếp

=>O,B,D,A cùng thuộc một đường tròn

b: Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

=>BA\(\perp\)CE tại A

Xét ΔBEC vuông tại B có BA là đường cao

nên \(CA\cdot CE=CB^2=\left(2R\right)^2=4R^2\)

c:

i: Xét (O) có

DA,DB là các tiếp tuyến

Do đó: DA=DB

=>D nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1),(2) suy ra OD là đường trung trực của AB

=>OD\(\perp\)AB tại K và K là trung điểm của AB

Xét tứ giác AKOI có \(\widehat{AKO}=\widehat{AIO}=\widehat{KAI}=90^0\)

nên AKOI là hình chữ nhật

=>OA=IK

=>IK=R

ii: ΔAHB vuông tại H

mà HK là đường trung tuyến

nên HK=KA=KB

=>K là tâm đường tròn ngoại tiếp ΔAHB

Gọi M là giao điểm của AO và KI

AKOI là hình chữ nhật

=>AO cắt KI tại trung điểm của mỗi đường

=>M là trung điểm chung của AO và KI

ΔAHO vuông tại H

mà HM là đường trung tuyến

nên \(HM=\dfrac{AO}{2}=\dfrac{KI}{2}\)

Xét ΔHKI có

HM là đường trung tuyến

HM=KI/2

Do đó: ΔHKI vuông tại H

=>HK\(\perp\)HI

Xét (K) có

HK là bán kính

HI\(\perp\)HK tại H

Do đó: HI là tiếp tuyến của (K)

=>HI là tiếp tuyến của đường tròn ngoại tiếp ΔHAB

iii: Vì \(\widehat{AHO}=\widehat{AKO}=\widehat{AIO}=90^0\)

nên A,H,K,O,I cùng thuộc đường tròn đường kính AO

trung bình cộng của 50 số lẻ liên tiếp là 50 . Số lớn nhất là?

Đổi 1 giờ 30 phút =3/2 giờ

1 giờ 25 phút =17/12 giờ

Gọi vận tốc cano khi nước lặng là x (km/h) và vận tốc dòng nước là y (km/h) với x;y>0

Vận tốc cano khi xuôi dòng: `x+y` (km/h)

Vận tốc cano khi ngược dòng: `x-y` (km/h)

Do cano xuôi dòng 40km và ngược dòng 15km hết 3/2 giờ nên ta có pt:

\(\dfrac{40}{x+y}+\dfrac{15}{x-y}=\dfrac{3}{2}\) (1)

Do cano xuôi dòng 30km và ngược dòng 20km hết 17/12 giờ nên ta có pt:

\(\dfrac{30}{x+y}+\dfrac{20}{x-y}=\dfrac{17}{12}\) (2)

Từ (1) và (2) ta có hệ:

\(\left\{{}\begin{matrix}\dfrac{40}{x+y}+\dfrac{15}{x-y}=\dfrac{3}{2}\\\dfrac{30}{x+y}+\dfrac{20}{x-y}=\dfrac{17}{12}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{40}\\\dfrac{1}{x-y}=\dfrac{1}{30}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+y=40\\x-y=30\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=35\\y=5\end{matrix}\right.\)

Shin là nhân vật chính trong bộ truyện tranh Shin cậu bé bút chì. Shin là một cậu bé 5 tuổi, có mái tóc xoăn vàng và luôn mang theo chiếc bút chì đặc biệt. Shin rất thông minh, nghịch ngợm và hài hước. Shin luôn muốn biến mọi thứ trở nên thú vị hơn và được mọi người yêu thích.

Shin là một người bạn tốt, luôn sẵn sàng giúp đỡ và chia sẻ với bạn bè. Shin có nhiều người bạn thân, nhưng người bạn thân nhất của Shin là Fujiko, một cô bé cũng có tính cách hài hước và thẳng thắn. Shin và Fujiko luôn ở bên nhau, cùng nhau chơi, học và trải qua những tình huống dễ thương và vui nhộn.

Shin cũng là một người con ngoan, luôn yêu thương và tôn trọng bố mẹ. Shin có một gia đình hạnh phúc, gồm bố là Hiroshi, mẹ là Misae và chị gái là Himawari. Shin thường gây ra những rắc rối cho bố mẹ, nhưng cũng thường làm cho bố mẹ cười và tự hào. Shin cũng rất thương em gái của mình, dù em gái thường hay chọc ghẹo Shin.

Shin là một nhân vật rất đáng yêu và khó quên. Em rất thích xem truyện tranh và hoạt hình về Shin. Em cảm thấy Shin giống như một người bạn của em, luôn mang lại niềm vui và bất ngờ cho em. Em mong muốn được gặp và chơi với Shin một lần. Em cũng muốn học hỏi từ Shin những điều tốt đẹp, như sự thông minh, nghịch ngợm và hài hước.

kudo shinichi mô 

Hoá trị các nguyên tố:

Ag = I

Al = III

Fe = II , III

Cu = I , II

K = I

S = II , IV , VI

P = III , V

C = IV , II ,...

N = II , III , IV ,..

Mg = II

Na = I

Zn = II 

Ca = II

Vẻ đẹp và số phận của những người phụ nữ xưa là.                                       Vẻ đẹp thùy mỵ , nết na ,trang hoà với bà con xóm làng. Thân phận của người phụ nữ trong xã hội phong kiến lúc bấy giờ rất thấp bé, không có tiếng nói, chồng muốn nói gì thì nói muốn làm gì thì làm, phụ nữ chính chuyên một chồng , đàn ông thì năm thê bảy thiếp.

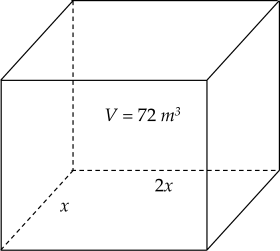
Diện tích đáy bể là: \(2x^2\) `(m^2)`

Chiều cao bể là: \(\dfrac{72}{2x^2}=\dfrac{36}{x^2}\left(m^2\right)\)

Diện tích xung quanh bể là: \(\left(2x+x\right).2.\dfrac{36}{x^2}=\dfrac{216}{x}\left(m^2\right)\)

Diện tích cần xây là:

\(2x^2+\dfrac{216}{x}=2\left(x^2+\dfrac{54}{x}+\dfrac{54}{x}\right)\ge2.3\sqrt[3]{x^2.\dfrac{54}{x}.\dfrac{54}{x}}=54\sqrt[3]{4}\left(m^2\right)\)

Dấu "=" xảy ra khi \(x^2=\dfrac{54}{x}\Rightarrow x=\sqrt[3]{54}=3,78\left(m\right)\)

a: Ta có: AM\(\perp\)AB

BP\(\perp\)AB

Do đó: AM//BP

Xet ΔOAM vuông tại A và ΔOBP vuông tại B có

OA=OB

\(\widehat{AOM}=\widehat{BOP}\)(hai góc đối đỉnh)

Do đó: ΔOAM=ΔOBP

=>OM=OP

b: Xét ΔNOM vuông tại O và ΔNOP vuông tại O có

NO chung

OM=OP

Do đó: ΔNOM=ΔNOP

=>\(\widehat{NMO}=\widehat{NPO}\)

=>\(\widehat{NMO}=\widehat{AMO}\)

=>MO là phân giác của góc AMN

Xét ΔMAO vuông tại A và ΔMHO vuông tại H có

MO chung

\(\widehat{AMO}=\widehat{HMO}\)

Do đó: ΔMAO=ΔMHO

=>OA=OH

=>OH=R

Xét (O) có

OH là bán kính

MN\(\perp\)OH tại H

Do đó: MN là tiếp tuyến của (O)

Xét (O) có

NH,NB là các tiếp tuyến

Do đó: NH=NB

ΔMAO=ΔMHO

=>MA=MH

Xét ΔOMN vuông tại O có OH là đường cao

nên \(HM\cdot HN=OH^2=R^2\)

=>\(MA\cdot BN=R^2\)