Tất tần tật về gp, coin, các em xem link dưới bình luận nhé.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y = 2\sqrt{1-x^2} + x^2 \) trên miền xác định của nó, ta thực hiện các bước sau:
1. **Xác định miền xác định của hàm số**:
\[
1 - x^2 \geq 0 \implies -1 \leq x \leq 1
\]
Do đó, hàm số xác định trên khoảng \([-1, 1]\).
2. **Tính đạo hàm của hàm số**:
\[
y = 2\sqrt{1 - x^2} + x^2
\]
Đạo hàm của hàm số \( y \) là:
\[
y' = \frac{d}{dx} \left( 2\sqrt{1 - x^2} + x^2 \right)
\]
Áp dụng quy tắc đạo hàm:
\[
y' = 2 \cdot \frac{d}{dx} \left( \sqrt{1 - x^2} \right) + \frac{d}{dx} \left( x^2 \right)
\]
\[
= 2 \cdot \frac{1}{2\sqrt{1 - x^2}} \cdot (-2x) + 2x
\]
\[
= -\frac{2x}{\sqrt{1 - x^2}} + 2x
\]
\[
= 2x \left(1 - \frac{1}{\sqrt{1 - x^2}}\right)
\]
3. **Tìm các điểm cực trị**:
Giải phương trình \( y' = 0 \):
\[
-\frac{2x}{\sqrt{1 - x^2}} + 2x = 0
\]
\[
2x \left( 1 - \frac{1}{\sqrt{1 - x^2}} \right) = 0
\]
\[
2x = 0 \quad \text{hoặc} \quad 1 - \frac{1}{\sqrt{1 - x^2}} = 0
\]
\[
x = 0 \quad \text{hoặc} \quad \sqrt{1 - x^2} = 1
\]
\[
x = 0 \quad \text{hoặc} \quad 1 - x^2 = 1
\]
\[
x = 0 \quad \text{hoặc} \quad x^2 = 0
\]
\[
x = 0
\]
4. **Xét giá trị của hàm số tại các điểm biên và điểm cực trị**:
\[
y(-1) = 2\sqrt{1 - (-1)^2} + (-1)^2 = 2\sqrt{0} + 1 = 1
\]
\[
y(1) = 2\sqrt{1 - 1^2} + 1^2 = 2\sqrt{0} + 1 = 1
\]
\[
y(0) = 2\sqrt{1 - 0^2} + 0^2 = 2\sqrt{1} + 0 = 2
\]
Vậy giá trị lớn nhất của hàm số trên khoảng \([-1, 1]\) là \( 2 \) và giá trị nhỏ nhất là \( 1 \).

Chứng minh không có nghiệm nguyên dương nhé chứ vẫn có nghiệm nguyên.

\(D=\left[0;2\right]\)
Có \(f'\left(x\right)=\dfrac{-x+1}{\sqrt{2x-x^2}},\forall x\in\left(0;2\right)\)
\(f'\left(x\right)=0\Leftrightarrow x=1\)
Vậy hàm số đã cho đồng biến trên \(\left(0;1\right)\) và nghịch biến trên \(\left(1;2\right)\)
ĐKXĐ: \(2x-x^2>=0\)
=>\(x^2-2x< =0\)
=>x(x-2)<=0
=>0<=x<=2
\(y=\sqrt{2x-x^2}\)
=>\(y'=\dfrac{\left(2x-x^2\right)'}{2\sqrt{2x-x^2}}=\dfrac{-2x+2}{2\sqrt{2x-x^2}}=\dfrac{-x+1}{\sqrt{2x-x^2}}\)
Đặt y'>0
=>-x+1>0
=>-x>-1
=>x<1
=>0<=x<1
=>Hàm số đồng biến khi 0<=x<1
Đặt y'<0
=>-x+1<0
=>-x<-1
=>x>1
=>1<x<=2
=>Hàm số nghịch biến khi 1<x<=2

Có vẻ hơi trễ:")
a)
\(n=3\Rightarrow\) có 3 lóp electron.
\(l=2\Rightarrow\) e cuối vào phân lớp 3d
\(m=1,m_s=-\dfrac{1}{2}\Rightarrow\) mũi tên hướng xuống dừng ở ô thứ 4.
=> e cuối của nguyên tố điền vào phân lớp \(3d^9\)
Cấu hình e bền vững sau bão hòa: \(1s^22s^22p^63s^23p^63d^{10}4s^1\left(Cu\right)\)
\(\Rightarrow\left\{{}\begin{matrix}STT:29\\CK:4\\nhóm:IB\end{matrix}\right.\)
b)
Tương tự câu a, e cuối của nguyên tố điền vào phân lóp \(4p^2\)
Cấu hình e: \(1s^22s^22p^63s^23p^63d^{10}4s^24p^2\left(Ge\right)\left\{{}\begin{matrix}STT:32\\CK:4\\nhóm:IVA\end{matrix}\right.\)

a) Vì \(p\) là snt lớn hơn 3 nên \(p⋮̸3\) \(\Rightarrow p^2\equiv1\left[3\right]\) hay \(p^2-1⋮3\)
b) Theo câu a), ta có \(p^2\equiv q^2\equiv1\left[3\right]\) nên \(p^2-q^2⋮3\)
c) Vì \(p,q\) là các snt lớn hơn 3 nên chúng cũng là các snt lẻ \(\Rightarrow p^2\equiv q^2\equiv1\left[8\right]\)
\(\Rightarrow p^2-q^2⋮8\)

Cho \(p=2,p=3\) ta thấy không thỏa mãn.
Cho \(p=5\) ta thấy thỏa mãn.
Xét \(p>5\), khi đó \(p⋮̸5\). Khi đó \(p^2\equiv1,4\left[5\right]\) (tính chất của scp)
Khi \(p^2\equiv1\left[5\right]\) thì \(p^2+1⋮5\), khi \(p^2\equiv4\left[5\right]\) thì \(p^2+6⋮5\) nên 1 trong 2 số này là hợp số, không thỏa mãn.
Vậy \(p=5\) là snt duy nhất thỏa mãn ycbt.
Đây là dạng toán nâng cao chuyên đề số nguyên tố, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau.
+ Nếu p = 2 ta có: p2 + 4 = 22 + 4 = 4 + 4 = 8 (loại)
+ Nếu p = 3 ta có: p2 + 6 = 32 + 6 = 9 + 6 = 15 (loại)
+ Nếu p = 5 ta có: p2 + 4 = 52 + 4 = 25 + 4 = 29 (thỏa mãn)
p2 + 6 = 52 + 6 = 25 + 6 = 31 (thỏa mãn)
+ Nếu p > 5 khi đó: p2 : 5 dư 1 hoặc 4 (tính chất số chính phương)
TH1 p2 : 5 dư 1 ⇒ p2 + 4 ⋮ 5 (là hợp số loại)
TH2 p2 : 5 dư 4 \(\Rightarrow\) p2 + 6 ⋮ 5 (là hợp số loại)
Từ những lập luận trên ta có:
p = 5 là giá trị số nguyên tố duy nhất thỏa mãn đề bài
Kết luận số nguyên tố thỏa mãn đề bài là 5.


ABCD là hình vuông nên OA=OC => d( A,(SBD) ) = d( C,(SBD) )
Kẻ AH vuông SO
BD vuông AO, BD vuông SA nên BD vuông (SAO) => BD vuông AH
=> AH vuông (SBD)
=> d( A,(SBD) ) = AH
Xét SAO : \(\dfrac{1}{AH^2}\) = \(\dfrac{1}{SA^2}\) + \(\dfrac{1}{AO^2}\)
SA = 3a, AO = \(a\sqrt{2}\) => AH = \(\dfrac{3a\sqrt{22}}{11}\)
Vậy khoảng cách từ C đến (SBD) = \(\dfrac{3a\sqrt{22}}{11}\)
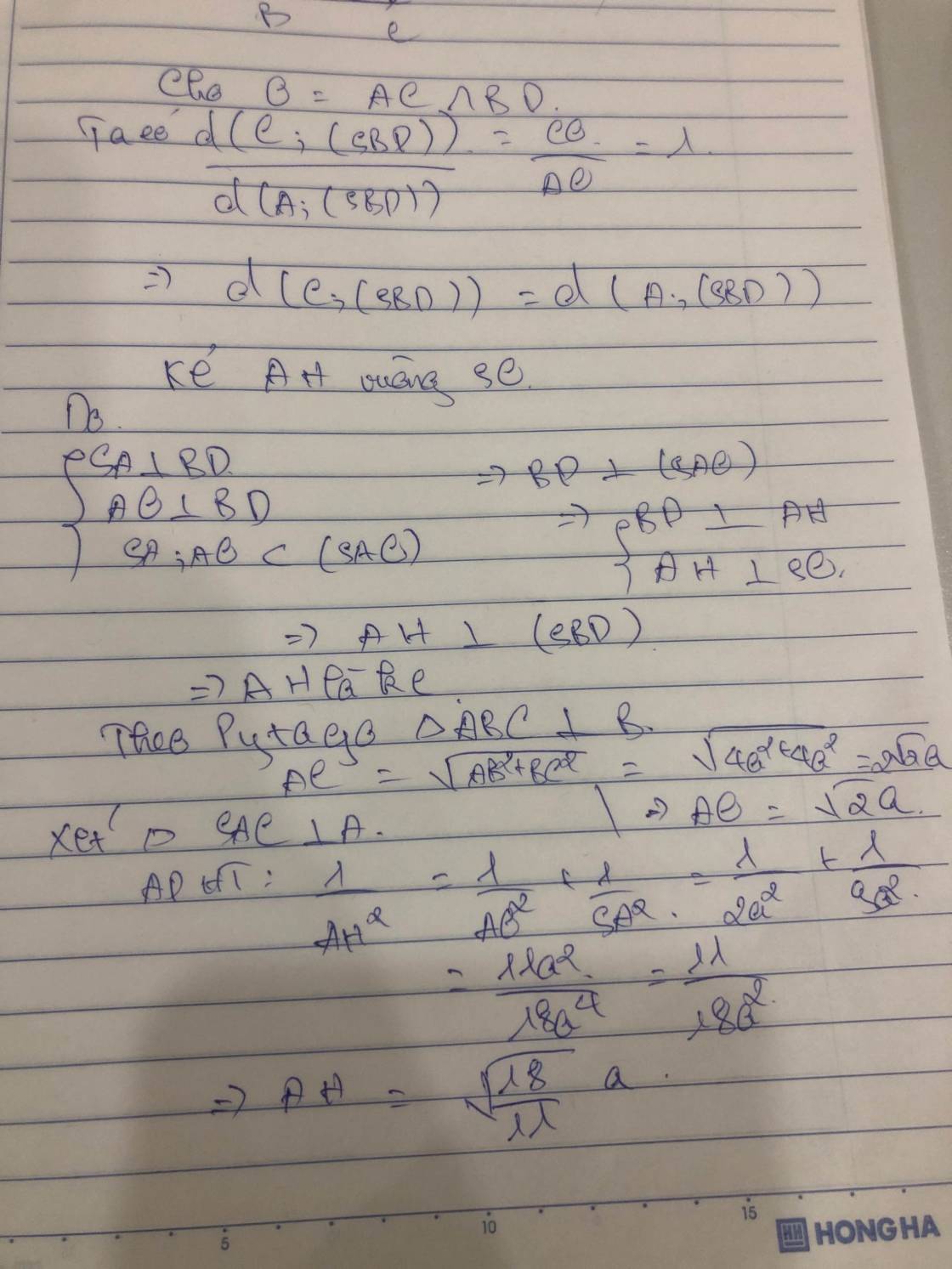
Em sẽ cố gắng để được nhiều GP để có thể nhận thưởng từ cô Hoài <3
https://olm.vn/cau-hoi/co-than-ai-chao-tat-ca-cac-thanh-vien-cua-olm-cam-on-cac-em-da-yeu-mendong-hanh-cung-olm-tren-hanh-trinh-tri-thuc-cuoc-song-cung-nhu-cac-dong-gop.8954441961523