giải phương trình : 2x2-5\(\sqrt{x^2_{ }-5x+7}\) =10x-17
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(\Delta ABC\) cân tại A, có AM là đường trung tuyến
\(\Rightarrow AM\) cũng là đường trung trực của \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
\(\Rightarrow\widehat{AMC}=90^0\)
Tứ giác \(AMCN\) có:
\(I\) là trung điểm của AC (gt)
\(I\) là trung điểm của MN (gt)
\(\Rightarrow AMCN\) là hình bình hành
Mà \(\widehat{AMC}=90^0\)
\(\Rightarrow AMCN\) là hình chữ nhật
b) Do \(AMCN\) là hình chữ nhật
\(\Rightarrow AN=CM\) và \(AN\) // \(CM\)
Do \(AN\) // \(CM\) (cmt)
\(\Rightarrow AN\) // \(BM\)
Do \(M\) là trung điểm của \(BC\) (gt)
\(\Rightarrow BM=CM\)
Mà \(AN=CM\left(cmt\right)\)
\(\Rightarrow BM=AN\)
Tứ giác \(ABMN\) có:
\(BM\) // \(AN\) (cmt)
\(BM=AN\left(cmt\right)\)
\(\Rightarrow ABMN\) là hình bình hành
Mà \(E\) là trung điểm của AM
\(\Rightarrow E\) là trung điểm của BN

Gọi x (tổ) là số tổ nhiều nhất có thể chia (x ∈ ℕ*)
⇒ x = ƯCLN(24; 108)
Ta có:
24 = 2³.3
108 = 2².3³
⇒ x = ƯCLN(24; 108) = 2².3 = 12
Vậy số tổ nhiều nhất có thể chia là 12 tổ
Gọi x (tổ) là số tổ nhiều nhất có thể chia (x ∈ ℕ*)
⇒ x = ƯCLN(24; 108)
Ta có:
24 = 2³.3
108 = 2².3³
⇒ x = ƯCLN(24; 108) = 2².3 = 12
Vậy số tổ nhiều nhất có thể chia là 12 tổ

47.63 = (55 - 8)(55 + 8)
= 55² - 8²
= 3025 - 64
= 2961
--------
47.(63 - 15) - 63.(47 - 15)
= 47.63 - 47.15 - 63.47 + 63.15
= 47.(63 - 63) + 15.(63 - 47)
= 47.0 + 15.16
= 0 + 240
= 240
47.63 = (55 - 8)(55 + 8)
= 55² - 8²
= 3025 - 64
= 2961
--------
47.(63 - 15) - 63.(47 - 15)
= 47.63 - 47.15 - 63.47 + 63.15
= 47.(63 - 63) + 15.(63 - 47)
= 47.0 + 15.16
= 0 + 240
= 240


Gọi x (đồng) là giá niêm yết của tivi (x > 0)
⇒ 24000000 - x (đồng) là giá niêm yết của máy lạnh
Giá tivi sau khi giảm:
x - 0,1x = 0,9x (đồng)
Giá máy lạnh sau khi giảm:
24000000 - x - (24000000 - x).0,25 = 24000000 - x - 6000000 + 0,25x = 18000000 - 0,75x (đồng)
Theo đề bài ta có phương trình:
0,9x + 18000000 - 0,75x = 20250000
⇔ 0,15x = 20250000 - 18000000
⇔ 0,15x = 2250000 (đồng)
⇔ x = 2250000 : 0,15
⇔ x = 15000000 (nhận)
Vậy giá niêm yết của tivi là 15000000
Giá niêm yết của máy lạnh là 24000000 - 15000000 = 9000000 (đồng)
Gọi x (đồng) là giá niêm yết của tivi (x > 0)
⇒ 24000000 - x (đồng) là giá niêm yết của máy lạnh
Giá tivi sau khi giảm:
x - 0,1x = 0,9x (đồng)
Giá máy lạnh sau khi giảm:
24000000 - x - (24000000 - x).0,25 = 24000000 - x - 6000000 + 0,25x = 18000000 - 0,75x (đồng)
Theo đề bài ta có phương trình:
0,9x + 18000000 - 0,75x = 20250000
⇔ 0,15x = 20250000 - 18000000
⇔ 0,15x = 2250000 (đồng)
⇔ x = 2250000 : 0,15
⇔ x = 15000000 (nhận)
Vậy giá niêm yết của tivi là 15000000
Giá niêm yết của máy lạnh là 24000000 - 15000000 = 9000000 (đồng)

(-6)² : 4 . 3 + 2 . 5² - 2019⁰
= 36 : 4 . 3 + 2 . 25 - 1
= 9 . 3 + 50 - 1
= 27 + 49
= 76

Tổng của hai số đó là:
158×2=316
Ta có sơ đồ:
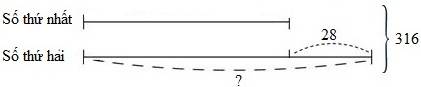
Số thứ hai là:
(316+28):2=172
Đáp số: 172.
Vậy đáp án đúng điền vào ô trống là 172.
tick cho mình nha mình nhanh nhất đó cảm ơn bạn nhiều nha

2\(x^2\) - 5 \(\sqrt{x^2-5x+7}\) = 10\(x\) - 17 Đk \(x^2\) - 5\(x\) + 7 ≥ 0
\(x^2\) - 2.\(\dfrac{5}{2}\)\(x\) + \(\dfrac{25}{4}\) + \(\dfrac{3}{4}\) = (\(x\) - \(\dfrac{5}{2}\))2 + \(\dfrac{3}{4}\) > 0 ∀ \(x\)
ta có: 2\(x^2\) - 5\(\sqrt{x^2-5x+7}\) = 10\(x\) - 17
2\(x^2\) - 5\(\sqrt{x^2-5x+7}\) - 10\(x\) + 17 = 0
(2\(x^2\) - 10\(x\) + 14) - 5\(\sqrt{x^2-5x+7}\) + 3 = 0
2.(\(x^2\) - 5\(x\) + 7) - 5.\(\sqrt{x^2-5x+7}\) + 3 = 0
Đặt \(\sqrt{x^2-5x+7}\) = y > 0 ta có:
2y2 - 5y + 3 = 0
2 + (-5) + 3 = 0
⇒ y1= 1; y2 = \(\dfrac{3}{2}\)
TH1 y = 1 ⇒ \(\sqrt{x^2-5x+7}\) = 1
⇒ \(x^2\) - 5\(x\) + 7 = 1
\(x^2\) - 5\(x\) + 6 = 0
\(\Delta\) = 25 - 24 = 49
\(x_1\) = \(\dfrac{-\left(-5\right)+\sqrt{1}}{2}\) = 3;
\(x_2\) = \(\dfrac{-\left(-5\right)-\sqrt{1}}{2}\) = 2;
TH2 y = \(\dfrac{3}{2}\)
\(\sqrt{x^2-5x+7}\) = \(\dfrac{3}{2}\)
\(x^2\) - 5\(x\) + 7 = \(\dfrac{9}{4}\)
4\(x^2\) - 20\(x\) + 28 = 9
4\(x^2\) - 20\(x\) + 19 = 0
\(\Delta'\) = 102 - 4.19
\(\Delta'\) = 24
\(x_1\) = \(\dfrac{-\left(-10\right)+\sqrt{24}}{4}\) = \(\dfrac{10+\sqrt{24}}{4}\)
\(x_2\) = \(\dfrac{-\left(-10\right)-\sqrt{24}}{4}\) = \(\dfrac{10-\sqrt{24}}{4}\)
8 - 5\(\sqrt{6}\)
Từ các lập luận trên kết luận phương trình có tập nghiệm là:
S = {8 - 5\(\sqrt{6}\); 2 ; 3; 8 + 5\(\sqrt{6}\)}
2�2x2 - 5 �2−5�+7x2−5x+7 = 10�x - 17 Đk �2x2 - 5�x + 7 ≥ 0
�2x2 - 2.5225�x + 254425 + 3443 = (�x - 5225)2 + 3443 > 0 ∀ �x
ta có: 2�2x2 - 5�2−5�+7x2−5x+7 = 10�x - 17
2�2x2 - 5�2−5�+7x2−5x+7 - 10�x + 17 = 0
(2�2x2 - 10�x + 14) - 5�2−5�+7x2−5x+7 + 3 = 0
2.(�2x2 - 5�x + 7) - 5.�2−5�+7x2−5x+7 + 3 = 0
Đặt �2−5�+7x2−5x+7 = y > 0 ta có:
2y2 - 5y + 3 = 0
2 + (-5) + 3 = 0
⇒ y1= 1; y2 = 3223
TH1 y = 1 ⇒ �2−5�+7x2−5x+7 = 1
⇒ �2x2 - 5�x + 7 = 1
�2x2 - 5�x + 6 = 0
ΔΔ = 25 - 24 = 49
�1x1 = −(−5)+122−(−5)+1 = 3;
�2x2 = −(−5)−122−(−5)−1 = 2;
TH2 y = 3223
�2−5�+7x2−5x+7 = 3223
�2x2 - 5�x + 7 = 9449
4�2x2 - 20�x + 28 = 9
4�2x2 - 20�x + 19 = 0
Δ′Δ′ = 102 - 4.19
Δ′Δ′ = 24
�1x1 = −(−10)+2444−(−10)+24 = 10+244410+24
�2x2 = −(−10)−2444−(−10)−24 = 10−244410−24
8 - 566
Từ các lập luận trên kết luận phương trình có tập nghiệm là:
S = {8 - 566; 2 ; 3; 8 + 566}