2x=2048
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NB
1
H9
HT.Phong (9A5)
CTVHS
5 tháng 8 2024
a) `2/3` của 14 là:
\(\dfrac{2}{3}\times14=\dfrac{28}{3}\)
b) `5/4` của 451 là:
\(\dfrac{5}{4}\times451=\dfrac{2255}{4}\)
c) Đổi: \(1\dfrac{1}{3}=\dfrac{4}{3}\)
`4/3` của 60:
\(\dfrac{4}{3}\times60=80\)
d) 23% của 50 là:
\(23\%\times50=11,5\)
5 tháng 8 2024
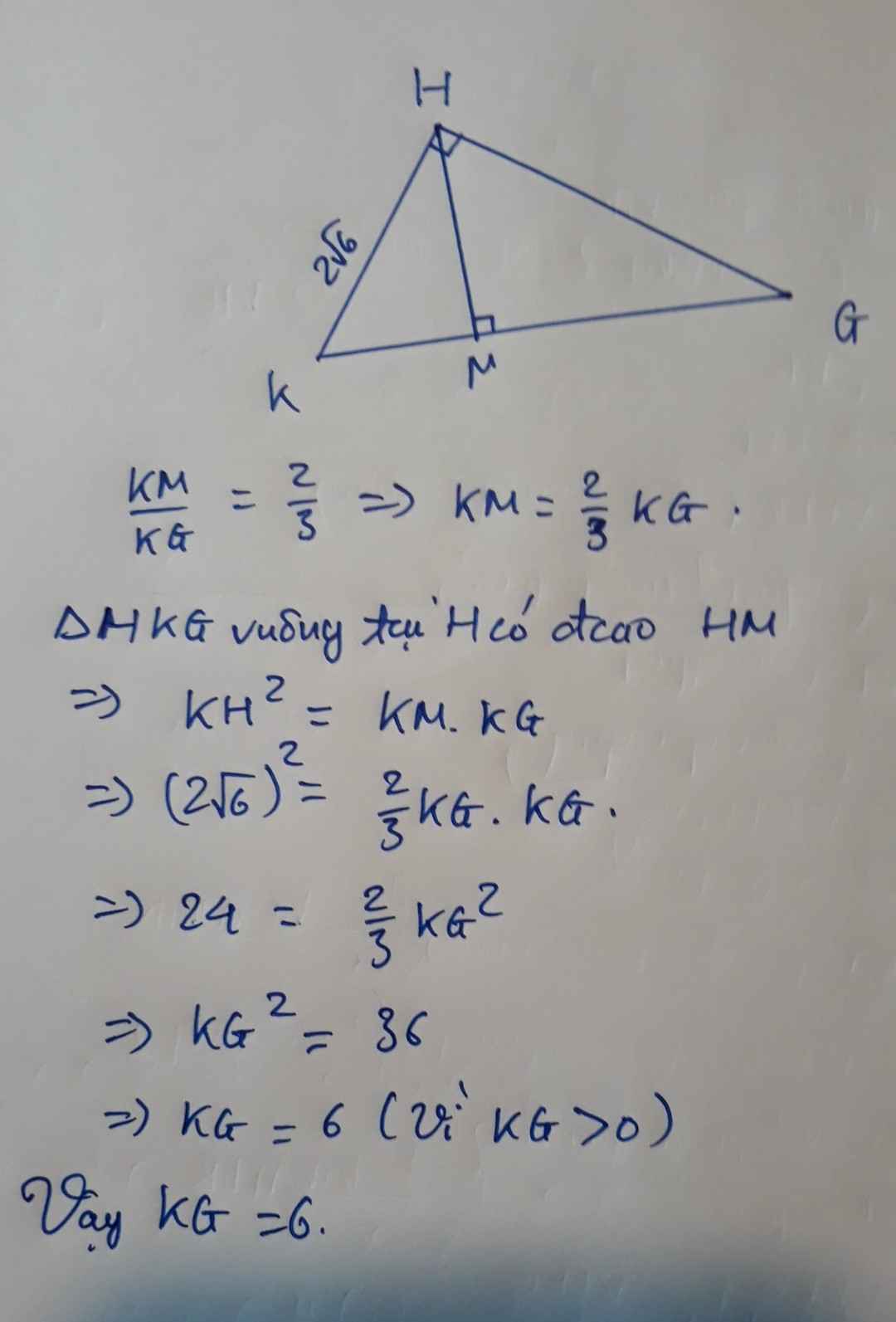
a: Xét ΔMAN và ΔMBC có
MA=MB
\(\widehat{AMN}=\widehat{BMC}\)(hai góc đối đỉnh)
MN=MC
Do đó: ΔMAN=ΔMBC
=>AN=BC
b: Xét ΔMBN và ΔMAC có
MB=MA
\(\widehat{BMN}=\widehat{AMC}\)(hai góc đối đỉnh)
MN=MC
Do đó: ΔMBN=ΔMAC
=>\(\widehat{MBN}=\widehat{MAC}\)
mà hai góc này là hai góc ở vị trí so le trong nên BN//AC
c: BN//AC
AB\(\perp\)AC
Do đó: BN\(\perp\)AB
TN
1
5 tháng 8 2024
\(5.3^x=15.3^5\)
\(5.3^x=5.3.3^5\)
\(5.3^x=5.3^6\)
\(3^x=3^6\)
\(x=6\)
PT
Phạm Trần Hoàng Anh
CTVHS
5 tháng 8 2024
`H=1+2.6+3.6^2+4.6^3+...+100.6^99`
`6H = 6+2.6^2+3.6^3+4.6^4+...+100.6^100`
`6H - H = (6+2.6^2+3.6^3+4.6^4+...+100.6^100)-(1+2.6+3.6^2+4.6^3+...+100.6^99)`
`5H = (6 - 2.6) + (2.6^2 - 3.6^2) + (3.6^3 - 4.6^3) + ... + (99. 6^99 - 100.6^99) + 100.6^100 - 1`
`5H = 100.6^100 - 1 + (-6) + (-6^2) + (-6^3) + ... + (-6^99)`
`5H = 100.6^100 - 1 - (6+6^2+6^3 + ... + 6^99)`
Đặt `S = 6+6^2+6^3 + ... + 6^99`
`6S = 6^2+6^3+6^4 + ... + 6^100`
`6S - S = (6^2+6^3+6^4 + ... + 6^100) - ( 6+6^2+6^3 + ... + 6^99)`
`5S = 6^100 - 6`
`S = ( 6^100 - 6)/5`
Khi đó: `5H = 100.6^100 - 1 - S`
`5H = 100.6^100 - 1 - ( 6^100 - 6)/5`
`5H = (500.6^100)/5 - 5/5 - ( 6^100 - 6)/5`
`5H = (500.6^100 - 5 - 6^100 + 6)/5`
`H = (499 . 6^100 + 1)/5`
Vậy ...
PT
Phạm Trần Hoàng Anh
CTVHS
4 tháng 8 2024
`S = 3^100 -3^99 +3^98 -3^97 +...+3^2 -3 +1`
`3S = 3^101 - 3^100 +3^99- 3^98+...+ 3^3 -3^2 +3`
`S + 3S = (3^100 -3^99 +3^98 -3^97 +...+3^2 -3 +1) + (3^101 - 3^100 +3^99- 3^98+...+ 3^3 -3^2 +3)`
`4S = 3^101 + (3^100 - 3^100) + (3^99 - 3^99) + ... + (3 - 3) + 1`
`4S = 3^101 + 1`
`S = (3^101 + 1)/4`
2x = 4048
=> x = 4048 : 2
=> x = 2024
Vậy x = 2024
x=1024