a: 2<3

=>\(2+8,5\cdot6< 3+8,5\cdot6\)

b: 2<3

=>\(\sqrt{2}< \sqrt{3}\)

=>\(-\sqrt{2}>-\sqrt{3}\)

=>\(30-\sqrt{2}>30-\sqrt{3}\)

c:

Vì 3>2

nên \(3\sqrt{3}>3\sqrt{2}\)

=>\(-3\sqrt{3}< -3\sqrt{2}\)

mà 35<36

nên \(35-3\sqrt{3}< 36-3\sqrt{2}\)

Bài 4:

a: 4x-y=1

=>y=4x-1

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=4x-1\end{matrix}\right.\)

b: x+3y=-2

=>x=-3y-2

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=-3y-2\end{matrix}\right.\)

Bài 5:

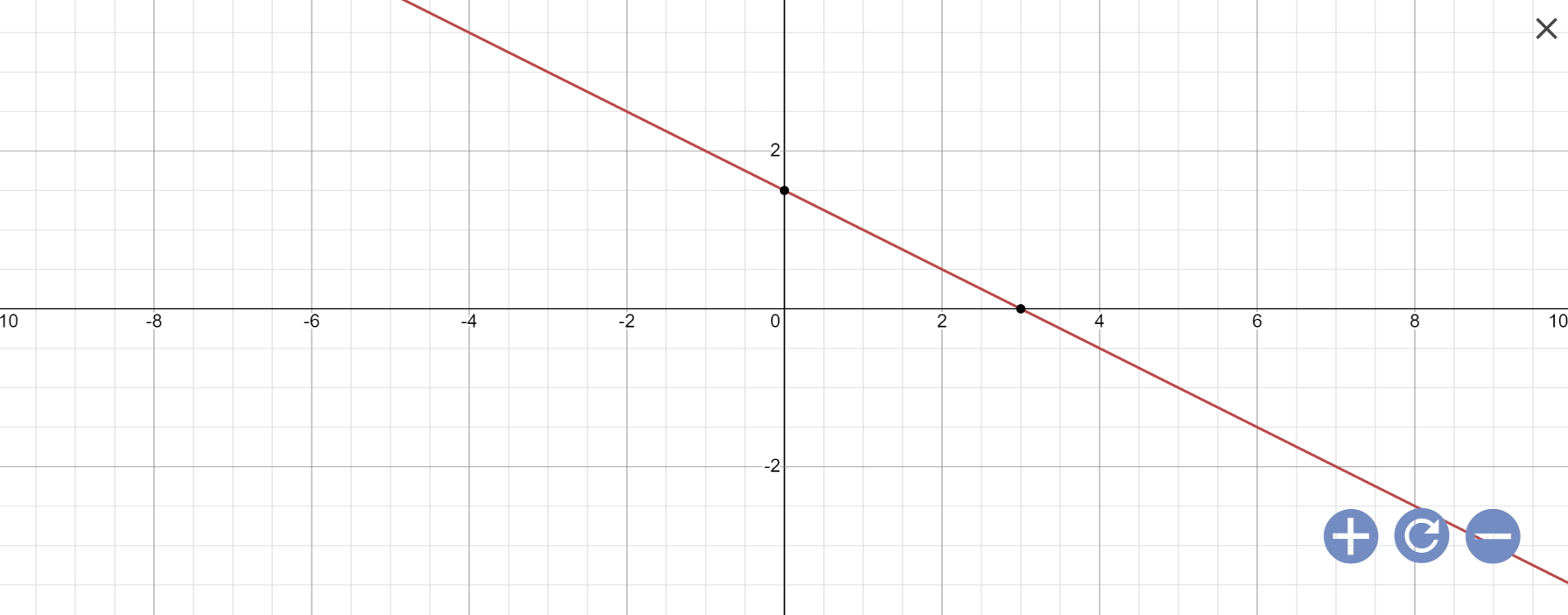
x+2y-3=0

=>2y=-x+3

=>\(y=\dfrac{-x+3}{2}\)

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{-x+3}{2}\end{matrix}\right.\)

Biểu diễn tập nghiệm: 

Biểu thức không có min bạn nhé. Bạn xem lại đề.

x² + 2y² +3xy - x - y + 3 = 0

(x² - y²) + (3y² + 3xy) - (x + y) = -3

(x - y)(x + y) + 3y(x + y) - (x + y) = -3

(x + y)(x + 2y -1) = -3 = 1.(-3) = (-1).3

(x;y)=(4;-3) (-6;5)

Lời giải:

$2(6x+7)^2(3x+4)(x+1)-12=0$

$\Leftrightarrow 2(36x^2+84x+49)(3x^2+7x+4)-12=0$

Đặt $3x^2+7x+4=a$ thì PT trở thành:

$2(12a+1)a-12=0$

$\Leftrightarrow 2a(12a+1)-12=0$

$\Leftrightarrow 24a^2+2a-12=0$

$\Leftrightarrow (24a^2-16a)+(18a-12)=0$

$\Leftrightarrow 8a(3a-2)+6(3a-2)=0$

$\Leftrightarrow (3a-2)(8a+6)=0$

$\Leftrightarrow (3a-2).2(4a+3)=0$

$\Leftrightarrow (3a-2)(4a+3)=0$

$\Rightarrow 3a-2=0$ hoặc $4a+3=0$

Nếu $3a-2=0$

$\Leftrightarrow 3(3x^2+7x+4)-2=0$

$\Leftrightarrow 9x^2+21x+10=0$

$\Leftrightarrow (3x+2)(3x+5)=0\Leftrightarrow x=\frac{-2}{3}$ hoặc $x=\frac{-5}{3}$

Nếu $4a+3=0$

$\Leftrightarrow 4(3x^2+7x+4)+3=0$

$\Leftrightarrow 12x^2+28x+19=0$

$\Leftrightarrow 12(x+\frac{7}{6})^2=\frac{-8}{3}<0$ (vô lý - loại)

Vậy..........

a: Ta có: \(AE=EB=\dfrac{AB}{2}\)

\(BF=FC=\dfrac{BC}{2}\)

\(DK=KC=\dfrac{DC}{2}\)

mà AB=BC=CD

nên AE=EB=BF=FC=DK=KC

Xét tứ giác AECK có

AE//CK

AE=CK

Do đó: AECK là hình bình hành

b: Xét ΔDCF vuông tại C và ΔCBE vuông tại B có

DC=CB

CF=BE

Do đó: ΔDCF=ΔCBE

=>\(\widehat{DFC}=\widehat{CEB}\)

mà \(\widehat{CEB}+\widehat{BCE}=90^0\)

nên \(\widehat{BCE}+\widehat{DFC}=90^0\)

=>CE\(\perp\)DF

a) \(\dfrac{12}{5}>\dfrac{10}{5}=2=\dfrac{4}{2}>\dfrac{3}{2}\) (Số 2 làm trung gian)

Hay \(\dfrac{12}{5}>\dfrac{3}{2}\)

b) Ta có: 

`2023 < 2024 =>` \(\dfrac{2023}{2024}< 1\)

`2026 > 2025 =>` \(\dfrac{2026}{2025}>1\)

=> \(\dfrac{2023}{2024}< 1< \dfrac{2026}{2025}\) (1 làm trung gian)

Hay \(\dfrac{2023}{2024}< \dfrac{2026}{2025}\)

a: \(\dfrac{12}{5}=2,4;\dfrac{3}{2}=1,5\)

mà 2,4>1,5

nên \(\dfrac{12}{5}>\dfrac{3}{2}\)

b: \(\dfrac{2023}{2024}< \dfrac{2024}{2024}=1;\dfrac{2026}{2025}>\dfrac{2025}{2025}=1\)

Do đó: \(\dfrac{2023}{2024}< \dfrac{2026}{2025}\)

a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BH\cdot BC=BA^2\)

b: Xét ΔAHB vuông tại H có HD là đường cao

nên \(AD\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HE là đường cao

nên \(AE\cdot AC=AH^2\left(2\right)\)

Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)

=>\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Xét ΔADE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔADE~ΔACB

đéo