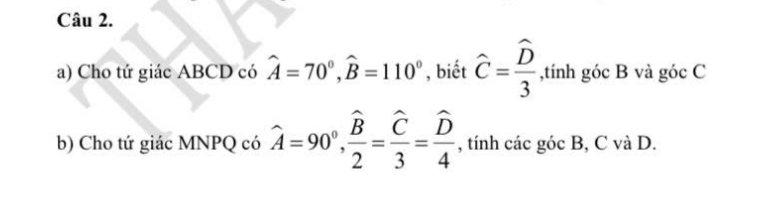
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AQHP có \(\widehat{AQH}=\widehat{APH}=\widehat{PAQ}=90^0\)
nên AQHP là hình chữ nhật
b: ΔCQH vuông tại Q
mà QK là đường trung tuyến
nên KQ=KH=KC
Xét ΔKQH có KQ=KH
nên ΔKQH cân tại K
Ta có: AQHP là hình chữ nhật
=>AH cắt QP tại trung điểm của mỗi đường và AH=PQ
=>O là trung điểm chung của AH và QP
=>OA=OH=OQ=OP
Ta có: OQ=OH
=>O nằm trên đường trung trực của QH(1)
Ta có: KQ=KH
=>K nằm trên đường trung trực của QH(2)
Từ (1),(2) suy ra OK là đường trung trực của QH
c: Ta có: OK là đường trung trực của QH
=>OK\(\perp\)QH
mà AC\(\perp\)QH
nên OK//AC
=>ACKO là hình thang
Để ACKO là hình thang cân thì \(\widehat{KCA}=\widehat{OAC}\)
=>\(\widehat{HAC}=\widehat{HCA}\)
=>ΔHAC cân tại H
mà ΔHAC vuông cân tại H
nên \(\widehat{ACH}=45^0\)
=>\(\widehat{ACB}=45^0\)

- Với n chẵn \(\Rightarrow n=2k\) với k nguyên
\(\Rightarrow n^2+2014=\left(2k\right)^2+2024=4k^2+2014=2\left(2k^2+1007\right)\)
Do \(2k^2+1007\) luôn lẻ \(\Rightarrow\)\(2\left(2k^2+1007\right)\) là số chia hết cho 2 nhưng ko chia hết cho 4 nên ko thể là SCP
\(\Rightarrow n^2+2014\) ko thể là SCP
- Với n lẻ \(\Rightarrow n=2k+1\)
\(\Rightarrow n^2+2014=\left(2k+1\right)^2+2014=4k^2+4k+2015=4\left(k^2+k+503\right)+3\)
\(\Rightarrow n^2+2014\) chia 4 dư 3
Mà 1 số chính phương chia 4 chỉ có thể dư 0 hoặc 1
\(\Rightarrow n^2+2014\) ko thể là SCP
Vậy \(n^2+2014\) ko là SCP với mọi n nguyên dương

Đặt \(n^2+2n+8=k^2\) với k là số tự nhiên
\(\Rightarrow\left(n^2+2n+1\right)+7=k^2\)
\(\Rightarrow\left(n+1\right)^2+7=k^2\)
\(\Rightarrow k^2-\left(n+1\right)^2=7\)
\(\Rightarrow\left(k+n+1\right)\left(k-n-1\right)=7\)
Ta có bảng sau:
| k+n+1 | -7 | -1 | 1 | 7 |
| k-n-1 | -1 | -7 | 7 | 1 |
| k | -4 | -4 | 4 | 4 |
| n | -4 | 2 | -4 | 2 |
Vậy \(n=\left\{-4;2\right\}\)

Gọi tam giác vuông cần tìm là ΔABC vuông tại A, AM là đường trung tuyến.
Trên tia đối của tia MA, lấy D sao cho MA=MD
=>M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
=>AD=BC
mà AD=2AM
nên BC=2AM
=>\(AM=\dfrac{1}{2}BC\)(ĐPCM)
(1-2x)(1+2x)-2(x+1)^2-(5-x)(x-3)
-3x(2x-x)+(1-2x)^2-(3x+1)^2-(2x-3)(2x+3)
giúp mình với
mình cần gấp


Ta có:
\(a^2+a+1=\left(a^2+2.a.\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(a+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall a\)
\(\Rightarrow\)PT đã cho vô nghiệm
Vậy không có giá trị \(a\) thỏa mãn \(P=a^{2014}+\dfrac{1}{a^{2014}}\)

Bài 1:
AB//CD
=>\(\widehat{A}+\widehat{D}=180^0\)
=>\(2\widehat{D}+\widehat{D}=180^0\)
=>\(3\cdot\widehat{D}=180^0\)
=>\(\widehat{D}=60^0\)
\(\widehat{A}=2\cdot60^0=120^0\)
AB//CD
=>\(\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{C}+\widehat{C}+40^0=180^0\)
=>\(2\cdot\widehat{C}=180^0-40^0=140^0\)
=>\(\widehat{C}=70^0\)
\(\widehat{B}=70^0+40^0=110^0\)
Bài 2:
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{BCK}\)
Do đó: ΔAHD=ΔBKC
=>DH=CK
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}+\widehat{D}=360^0-110^0-70^0=180^0\)
=>\(\dfrac{1}{3}\cdot\widehat{D}+\widehat{D}=180^0\)
=>\(\dfrac{4}{3}\cdot\widehat{D}=180^0\)
=>\(\widehat{D}=135^0\)
\(\widehat{C}=\dfrac{1}{3}\cdot135^0=45^0\)
b:
Sửa đề: Cho tứ giác ABCD.
Đặt \(\widehat{B}=x;\widehat{C}=y;\widehat{D}=z\)
\(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+y+z=360^0-90^0=270^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{270}{9}=30^0\)
=>\(x=2\cdot30^0=60^0;y=3\cdot30^0=90^0;z=4\cdot30^0=120^0\)
Vậy: \(\widehat{B}=x=60^0;\widehat{C}=y=90^0;\widehat{D}=z=120^0\)