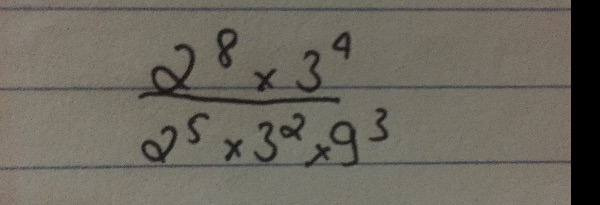
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) aAc và bBA
b) Góc BAD đối đỉnh với góc aAc => Góc BAD = 123o
c) aAc kề bù cAD => cAD = 180o - 123o =57o
Hai góc đồng vị bằng nhau => Hai cạnh a và b song song
d) a // b mà a vuông góc d => b cũng vuông góc d
Nhớ ti.ckk cho mình nha

Gọi các cạnh của tam giác lần lượt là a ; b và c ( cm ) tỉ lệ lần lượt với 3 ; 4 và 5
Theo bài ra , ta có :
a + b + c = 48
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{48}{12}=4\)
\(\Rightarrow\hept{\begin{cases}a=4.3=12\\b=4.4=16\\c=4.5=20\end{cases}}\)

\(2a=6b\Leftrightarrow\frac{a}{6}=\frac{b}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{a}{6}=\frac{b}{2}=\frac{a+b}{6+2}=-\frac{48}{8}=-5\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{6}=\left(-5\right)\Rightarrow a=\left(-30\right)\\\frac{b}{2}=\left(-5\right)\Rightarrow b=\left(-10\right)\end{cases}}\)
Từ \(2a=6b\)\(\Rightarrow\)\(\frac{a}{6}=\frac{b}{2}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{a}{6}=\frac{b}{2}=\frac{a+b}{6+2}=\frac{-48}{8}=-6\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{6}=-6\\\frac{b}{2}=-6\end{cases}}\)\(\Rightarrow\hept{\begin{cases}a=-36\\b=-12\end{cases}}\)

\(\frac{2^8.3^4}{2^5.3^2.9^3}\)=\(\frac{2^3.3^2}{1.1.\left(3^2\right)^3}\)=\(\frac{8.3^2}{3^6}\)=\(\frac{8.1}{3^4}\)=\(\frac{8}{81}\)


Vì a + b + c ≠ 0 , áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
\(\Rightarrow\hept{\begin{cases}a=1.b=b\\b=1.c=c\\c=1.a=a\end{cases}}\Rightarrow a=b=c\)
Khi đó \(P=\frac{a^{49}.b^{51}}{c^{100}}=\frac{c^{49}.c^{51}}{c^{100}}=\frac{c^{100}}{c^{100}}=1\)( do a = b = c )
Vậy P = 1
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
\(\Rightarrow\)\(a=b;b=c;c=a\Leftrightarrow a=b=c\)
Suy ra:
\(\frac{a^{49}.b^{51}}{c^{100}}=\frac{a^{49}.a^{51}}{a^{100}}=\frac{a^{100}}{a^{100}}=1\)
Vậy: \(P=1\)
 giúp mình với
giúp mình với