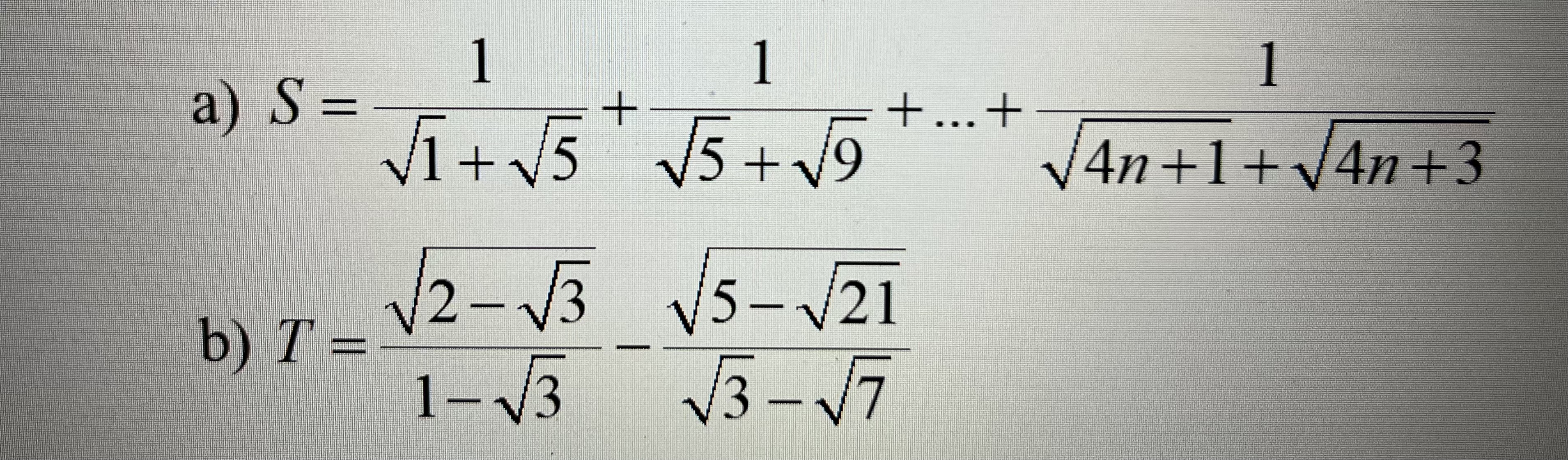Viết PTHH thể hiện tính chất của glucose và saccharose, tinh bột và cellulose
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)


Lệ Bình, một cái tên không quá xa lạ trong văn đàn Việt Nam, là người con gái mang trong mình tình yêu tha thiết với quê hương và những giá trị truyền thống tốt đẹp. Thơ của bà thường giản dị, chân chất, nhưng lại chứa đựng một sức lay động sâu sắc, chạm đến trái tim của người đọc. Trong số những tác phẩm nổi bật của Lệ Bình, bài thơ "Thăm Ngoại" được xem như một khúc ca ngọt ngào, du dương về tình cảm gia đình ấm áp, về vẻ đẹp bình dị của làng quê Việt Nam, và về những rung động tinh tế trong tâm hồn con người. Bài viết này sẽ đi sâu phân tích những giá trị nội dung và nghệ thuật đặc sắc của bài thơ, để thấy được tài năng và tấm lòng của nữ sĩ Lệ Bình.
Ngay từ những dòng thơ đầu tiên, "Thăm Ngoại" đã mở ra một không gian làng quê thân thương, gần gũi. Đó là một buổi trưa hè oi ả, nhưng lại được xoa dịu bởi bóng mát của cây đa cổ thụ:
> "Trưa hè bóng cả cây đa
>
> Giếng khơi mát ngọt đậm đà tình quê"
Cây đa, giếng nước là những hình ảnh quen thuộc, gắn liền với đời sống của người dân Việt Nam từ bao đời nay. Dưới bóng cây đa, người ta tìm thấy sự bình yên, thư thái, là nơi để nghỉ ngơi, trò chuyện sau những giờ lao động vất vả. Giếng nước khơi gợi cảm giác mát lành, trong trẻo, là nguồn nước nuôi dưỡng sự sống, là biểu tượng của sự thanh khiết, tinh túy. Chỉ với vài nét phác họa đơn sơ, Lệ Bình đã tái hiện thành công một bức tranh làng quê thanh bình, yên ả, đậm đà bản sắc văn hóa dân tộc.
Điểm nhấn của bài thơ chính là hình ảnh người bà - trung tâm của tình yêu thương và sự ấm áp gia đình. Bà hiện lên với những nét giản dị, mộc mạc, nhưng lại toát lên vẻ đẹp của sự hiền từ, nhân hậu:
> "Bà ngồi quạt mát ru cháu ngủ
>
> Tay nhăn nheo kể chuyện ngày xưa"
Hình ảnh bà ngồi quạt mát cho cháu ngủ gợi lên một cảm giác bình yên, ấm áp đến lạ thường. Bàn tay nhăn nheo của bà là dấu ấn của thời gian, của những vất vả, gian truân trong cuộc đời, nhưng cũng là biểu tượng của sự chở che, bao bọc. Những câu chuyện ngày xưa bà kể cho cháu nghe không chỉ là những bài học về đạo lý, về cách sống, mà còn là những ký ức, những giá trị văn hóa được truyền lại từ đời này sang đời khác.
Tình cảm của người cháu đối với bà được thể hiện một cách chân thành, xúc động qua từng câu chữ. Đó là sự yêu thương, kính trọng, biết ơn vô bờ bến:
> "Cháu về thăm ngoại lòng vui sướng
>
> Nhớ lời bà dặn sống phải thảo ngay"
Niềm vui sướng khi được về thăm ngoại thể hiện sự gắn bó sâu sắc của cháu với quê hương và gia đình. Lời bà dặn sống phải thảo ngay là lời dạy bảo thiêng liêng, là kim chỉ nam cho cháu trên con đường đời. Những lời dặn dò ấy không chỉ thể hiện sự quan tâm, lo lắng của bà dành cho cháu, mà còn là sự kỳ vọng của bà về một tương lai tốt đẹp cho cháu.
Không chỉ vậy, "Thăm Ngoại" còn là một bài thơ giàu chất trữ tình, thể hiện những rung động tinh tế trong tâm hồn tác giả. Đó là sự hòa quyện giữa tình yêu quê hương và tình cảm gia đình, là sự trân trọng những giá trị văn hóa truyền thống. Lệ Bình đã khéo léo sử dụng những hình ảnh, biểu tượng quen thuộc của làng quê Việt Nam để thể hiện những cảm xúc sâu lắng của mình.
Về mặt nghệ thuật, "Thăm Ngoại" là một bài thơ lục bát giản dị, mộc mạc, nhưng lại có sức lan tỏa mạnh mẽ. Thể thơ lục bát với nhịp điệu nhẹ nhàng, uyển chuyển đã góp phần tạo nên âm hưởng du dương, ngọt ngào cho bài thơ. Ngôn ngữ thơ trong sáng, giản dị, gần gũi với đời sống hàng ngày, dễ dàng đi vào lòng người đọc. Lệ Bình đã sử dụng thành công các biện pháp tu từ như so sánh, ẩn dụ, nhân hóa để tăng tính biểu cảm cho bài thơ, giúp người đọc hình dung rõ hơn về khung cảnh làng quê và cảm nhận sâu sắc hơn về tình cảm của tác giả.
Ví dụ, hình ảnh "Giếng khơi mát ngọt đậm đà tình quê" là một phép ẩn dụ tinh tế, gợi lên sự gắn bó mật thiết giữa con người với quê hương. Nước giếng không chỉ là nguồn nước để uống, để sinh hoạt, mà còn là biểu tượng của tình yêu thương, sự chở che của quê hương dành cho mỗi người. Hay hình ảnh "Bà ngồi quạt mát ru cháu ngủ" là một phép nhân hóa đặc sắc, giúp người đọc cảm nhận được sự ấm áp, dịu dàng của tình bà cháu.
Nhịp điệu của bài thơ cũng được Lệ Bình sử dụng một cách khéo léo, tạo nên sự hài hòa, cân đối cho toàn bộ tác phẩm. Sự phối hợp giữa các thanh điệu bằng trắc đã góp phần tạo nên âm hưởng riêng cho bài thơ, khiến cho người đọc cảm thấy thư thái, dễ chịu khi đọc.
Tóm lại, bài thơ "Thăm Ngoại" của Lệ Bình là một tác phẩm xuất sắc, thể hiện thành công tình cảm gia đình ấm áp, vẻ đẹp bình dị của làng quê Việt Nam và những rung động tinh tế trong tâm hồn con người. Với ngôn ngữ giản dị, hình ảnh thơ gần gũi, nhịp điệu du dương, "Thăm Ngoại" đã chinh phục trái tim của biết bao thế hệ độc giả. Bài thơ không chỉ là một kỷ niệm đẹp về tuổi thơ, về quê hương, mà còn là một lời nhắc nhở về những giá trị truyền thống tốt đẹp của dân tộc, về tình yêu thương, sự gắn bó giữa các thành viên trong gia đình. "Thăm Ngoại" xứng đáng là một trong những tác phẩm tiêu biểu của thơ ca Việt Nam hiện đại, góp phần làm phong phú thêm kho tàng văn học nước nhà. Đọc "Thăm Ngoại", ta như được trở về với cội nguồn, với những gì thân thương, giản dị nhất của cuộc đời, để rồi thêm yêu, thêm trân trọng những giá trị mà mình đang có.

Bàn về quan niệm "Sống là cho đâu chỉ nhận riêng mình"
Câu thơ của Tố Hữu “Sống là cho đâu chỉ nhận riêng mình” không chỉ biểu hiện một quan niệm sống cao đẹp mà còn truyền tải thông điệp nhân văn sâu sắc trong quan hệ giữa con người với con người. Câu thơ mời gọi mỗi chúng ta suy nghĩ về giá trị của việc sống vì người khác, vì cộng đồng, để làm cho cuộc sống trở nên ý nghĩa hơn.
Khái niệm "cho" và "nhận"
Trước hết, từ “cho” trong câu thơ không chỉ đơn thuần là việc ban tặng hay sẻ chia vật chất mà còn thể hiện sự đồng cảm, tình yêu thương và lòng nhân ái. Khi chúng ta cho đi, chúng ta không chỉ đem lại niềm vui, hạnh phúc cho người khác mà còn giúp tâm hồn mình tràn đầy ánh sáng. Những hành động nhỏ bé như giúp đỡ người già, tình nguyện tham gia các hoạt động từ thiện hay đơn giản là những lời động viên khó khăn cũng đều mang ý nghĩa lớn.
Ngược lại, "nhận" không chỉ là việc tiếp nhận những gì từ người khác hay cuộc sống ban tặng. Khi ta biết “nhận”, đồng nghĩa với việc ta cũng phải biết cảm ơn, trân trọng những điều xung quanh. Sự “nhận” cũng chỉ có ý nghĩa khi đi kèm với việc chúng ta có trách nhiệm chia sẻ lại cho cộng đồng.
Mối quan hệ giữa "cho" và "nhận"
“Sống là cho đâu chỉ nhận riêng mình” thể hiện một cách sống hài hòa giữa “cho” và “nhận”. Như quy luật của cuộc sống, đã cho đi thì cũng phải nhận lại. Cho đi những gì tốt đẹp để nhận lại những giá trị tinh thần vô hình mà có thể chúng ta chưa thể thấy ngay. Khi ta thực sự yêu thương và giúp đỡ người khác, ta không chỉ tạo ra niềm vui cho họ mà còn cho chính mình sự thanh thản, an lạc trong tâm hồn.
Ý nghĩa của việc sống vì người khác
Mối liên hệ giữa cho và nhận trong cuộc sống rất quan trọng, khi chúng ta nhìn sâu vào những tác động tích cực từ việc rèn luyện lối sống này. Những tấm gương như bác sĩ, thầy cô giáo, các tình nguyện viên... luôn tận tâm chăm sóc, dạy dỗ và hỗ trợ người khác mà không hề đòi hỏi một sự đền đáp xứng đáng nào. Những hành động cao đẹp của họ đã góp phần lớn vào việc xây dựng xã hội văn minh, tình người ấm áp.
Thế nhưng, không phải ai cũng nhận thức rõ về giá trị và ý nghĩa của việc cho đi. Vẫn còn nhiều người sống ích kỷ, chỉ nghĩ đến bản thân, coi mọi thứ như điều hiển nhiên. Họ quên rằng trong cuộc sống, mỗi người đều có những khó khăn riêng, và chỉ khi chúng ta biết mở lòng, chia sẻ, thì cuộc sống mới thực sự tươi đẹp hơn.
Kết luận
Tóm lại, quan niệm “Sống là cho đâu chỉ nhận riêng mình” như một lời nhắc nhở sâu sắc về cách sống đáng trân trọng. Chính nhờ việc yêu thương, sẻ chia và cống hiến cho người khác, chúng ta không chỉ tạo ra những mảnh ghép đẹp cho cuộc sống của mình mà còn đóng góp vào việc xây dựng một xã hội hài hòa, đủ đầy tình yêu thương. Hãy sống vì những điều tốt đẹp, sống để cho đi và cùng nhau xây dựng một tương lai tươi sáng hơn. Điều này không chỉ làm cho cuộc sống của ta thêm phong phú mà còn giúp nhân loại trở nên gắn bó, đoàn kết hơn bao giờ hết.
Chúng ta hãy nhớ rằng, chỉ khi biết cho đi, chúng ta mới thực sự nhận lại được những giá trị đẹp đẽ trong cuộc sống.

\(\text{Δ}=5^2-4\left(m-3\right)=25-4m+12=-4m+37\)
Để phương trình có hai nghiệm thì Δ>=0
=>-4m+37>=0
=>-4m>=-37
=>\(m< =\dfrac{37}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-5\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(2x_1x_2-\left(x_1+x_2\right)=2\)
=>\(2\left(m-3\right)-\left(-5\right)=2\)
=>2m-6+5=2
=>2m-1=2
=>2m=3
=>\(m=\dfrac{3}{2}\left(nhận\right)\)

a: Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên OBAC là tứ giác nội tiếp
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(4)
Từ (3),(4) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD
mà OA\(\perp\)BC
nên OA//CD
c: Sửa đề: Đường thẳng qua O vuông góc với AD cắt BC tại E
Gọi H là giao điểm của BC và OA
Vì OA là đường trung trực của BC
nên OA\(\perp\)BC tại H và H là trung điểm của BC
Gọi I là giao điểm của OE và DA
Theo đề, ta có: OE\(\perp\)DA tại I
Xét ΔOIA vuông tại I và ΔOHE vuông tại H có
\(\widehat{IOA}\) chung
Do đó: ΔOIA~ΔOHE
=>\(\dfrac{OI}{OH}=\dfrac{OA}{OE}\)
=>\(OI\cdot OE=OH\cdot OA\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\left(2\right)\)
Từ (1),(2) suy ra \(OI\cdot OE=R^2=OD^2\)
=>\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)
Xét ΔOID và ΔODE có
\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)
\(\widehat{IOD}\) chung
Do đó: ΔOID~ΔODE
=>\(\widehat{OID}=\widehat{ODE}\)
=>\(\widehat{ODE}=90^0\)
=>DE là tiếp tuyến của (O)