(3x-4y)^4 +|3y-4z|^5 +|x^2+y^2+z^2-1|=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2}{3}:\left(x-\dfrac{1}{3}\right)^3-9=\dfrac{23}{3}\)
=>\(\dfrac{2}{3}:\left(x-\dfrac{1}{3}\right)^3=\dfrac{23}{3}+9=\dfrac{50}{3}\)
=>\(\left(x-\dfrac{1}{3}\right)^3=\dfrac{2}{3}:\dfrac{50}{3}=\dfrac{2}{50}=\dfrac{1}{25}\)
=>\(x-\dfrac{1}{3}=\dfrac{\sqrt[3]{5}}{5}\)
=>\(x=\dfrac{\sqrt[3]{5}}{5}+\dfrac{1}{3}=\dfrac{3\sqrt[3]{5}+5}{15}\)

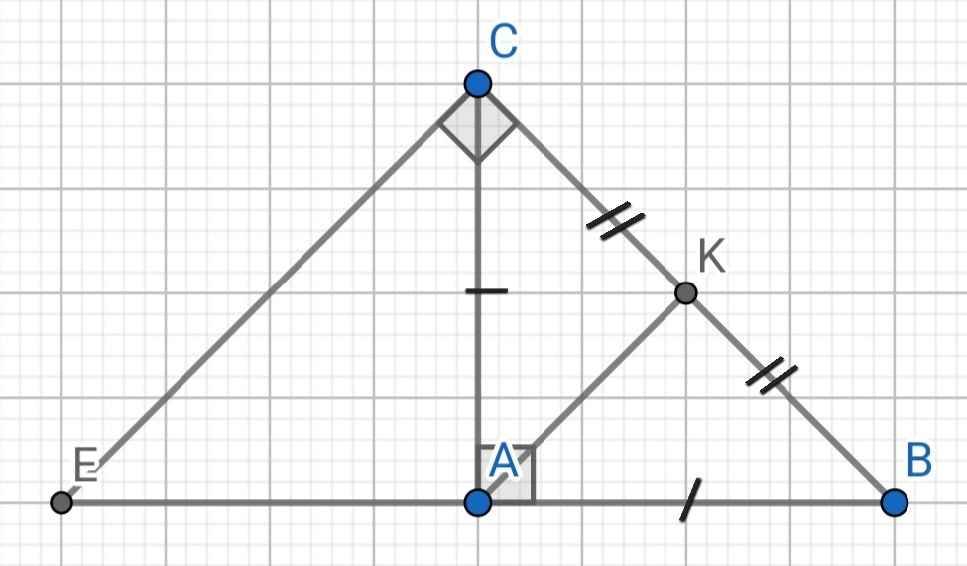
a) Do K là trung điểm của BC (gt)
⇒ KB = KC
Xét ∆AKB và ∆AKC có:
AK là cạnh chung
AB = AC (gt)
KB = KC (cmt)
⇒ ∆AKB = ∆AKC (c-c-c)
⇒ ∠AKB = ∠AKC (hai góc tương ứng)
Mà ∠AKB + ∠AKC = 180⁰ (kề bù)
⇒ ∠AKB = ∠AKC = 180⁰ : 2 = 90⁰
⇒ AK ⊥ BC
b) Do ∆ABC vuông tại A (gt)
AB = AC (gt)
⇒ ∆ABC vuông cân tại A
⇒ ∠ABC + ∠ACB = 90⁰
⇒ ∠ABC = ∠ACB = 90⁰ : 2 = 45⁰
⇒ ∠ACE = 90⁰ - ∠ACB
= 90⁰ - 45⁰
= 45⁰
⇒ ∠ACE = ∠ACB = 45⁰
⇒ CA là tia phân giác của ∠BCE
⇒ CA là đường phân giác của ∆BCE
Lại có CA ⊥ AB (∆ABC vuông tại A)
⇒ CA ⊥ BE
⇒ CA là đường cao của ∆BCE
∆BCE có:
CA là đường cao của ∆BCE
CA là đường phân giác của ∆BCE
⇒ ∆BCE cân tại C
⇒ CE = CB
c) ∆AKB vuông tại K
⇒ ∠KAC + ∠ACK = 90⁰
⇒ ∠KAC = 90⁰ - ∠ACK
= 90⁰ - ∠ACB
= 90⁰ - 45⁰
= 45⁰
⇒ ∠KAC = ∠ACK = 45⁰
⇒ ∆AKC cân tại K
⇒ AK = KC
Mà KC < BC (do K là trung điểm của BC)
⇒ AK < BC
Mà BC = EC (cmt)
⇒ AK < EC

Lời giải:
Vì $y^2\geq 0$ với mọi $y$ nên $14(x-2023)^2=26-3y^2\leq 26$
$\Rightarrow (x-2023)^2\leq \frac{26}{14}< 2$
Mà $(x-2023)^2$ là scp nên $(x-2023)^2=0$ hoặc $(x-2023)^2=1$
Nếu $(x-2023)^2=0$ thì: $26-3y^2=0\Rightarrow y^2=\frac{26}{3}$ (vô lý - loại)
Nếu $(x-2023)^2=1$ thì:
$x-2023=\pm 1\Rightarrow x=2022$ hoặc $x=2024$
$26-3y^2=14\Rightarrow 3y^2=12\Rightarrow y^2=4\Rightarrow y=\pm 2$
Vậy $(x,y)=(2022, 2), (2022, -2), (2024,2), (2024,-2)$

\(\dfrac{2}{3}x=\dfrac{3}{4}y=\dfrac{4}{5}z\Rightarrow\dfrac{x}{18}=\dfrac{y}{16}=\dfrac{z}{15}=\dfrac{x+y+z}{18+16+15}=\dfrac{57}{49}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{57}{49}.18=\dfrac{1026}{49}\\y=\dfrac{57}{49}.16=\dfrac{912}{49}\\z=\dfrac{57}{49}.15=\dfrac{855}{49}\end{matrix}\right.\)

Đặt \(\widehat{A}=a;\widehat{B}=b;\widehat{C}=c\)
Số đo góc A bằng 6 lần số đo góc B bằng 3 lần số đo góc C
=>a=6b=3c
=>\(\dfrac{a}{6}=\dfrac{6b}{6}=\dfrac{3c}{6}\)
=>\(\dfrac{a}{6}=\dfrac{b}{1}=\dfrac{c}{2}\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(a+b+c=180^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{1}=\dfrac{c}{2}=\dfrac{a+b+c}{6+1+2}=\dfrac{180}{9}=20\)
=>\(a=20\cdot6=120;b=1\cdot20=20;c=2\cdot20=40\)
Vậy: \(\widehat{A}=120^0;\widehat{B}=20^0;\widehat{C}=40^0\)
Lời giải:
Ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180^0$ (tổng 3 góc trong 1 tam giác)
Áp dụng TCDTSBN:
$\widehat{A}=6\widehat{B}=3\widehat{C}=\frac{\widehat{A}}{1}=\frac{\widehat{B}}{\frac{1}{6}}=\frac{\widehat{C}}{\frac{1}{3}}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+\frac{1}{6}+\frac{1}{3}}=\frac{180^0}{\frac{3}{2}}=120^0$
$\Rightarrow \widehat{A}=120^0; \widehat{B}=120^0:6=20^0; \widehat{C}=120^0:3=40^0$


\(\left(3x-4y\right)^4>=0\forall x,y\)
\(\left|3y-4z\right|^5>=0\forall y,z\)
\(\left|x^2+y^2+z^2-1\right|>=0\forall x,y,z\)
Do đó: \(\left(3x-4y\right)^4+\left|3y-4z\right|^5+\left|x^2+y^2+z^2-1\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}3x-4y=0\\3y-4z=0\\x^2+y^2+z^2=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{x}{4}=\dfrac{y}{3}\\\dfrac{y}{4}=\dfrac{z}{3}\\x^2+y^2+z^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{16}=\dfrac{y}{12}=\dfrac{z}{9}\\x^2+y^2+z^2=1\\\end{matrix}\right.\)
Đặt \(\dfrac{x}{16}=\dfrac{y}{12}=\dfrac{z}{9}=k\)
=>\(x=16k;y=12k;z=9k\)
\(x^2+y^2+z^2=1\)
=>\(256k^2+144k^2+81k^2=1\)
=>\(481k^2=1\)
=>\(k^2=\dfrac{1}{481}\)
=>\(k=\pm\dfrac{1}{\sqrt{481}}\)
TH1: \(k=\dfrac{1}{\sqrt{481}}\)
=>\(x=16\cdot\dfrac{1}{\sqrt{481}}=\dfrac{16}{\sqrt{481}};y=12\cdot\dfrac{1}{\sqrt{481}}=\dfrac{12}{\sqrt{481}};z=9\cdot\dfrac{1}{\sqrt{481}}=\dfrac{9}{\sqrt{481}}\)
TH2: \(k=-\dfrac{1}{\sqrt{481}}\)
=>\(x=-16\cdot\dfrac{1}{\sqrt{481}}=\dfrac{-16}{\sqrt{481}};y=12\cdot\dfrac{-1}{\sqrt{481}}=\dfrac{-12}{\sqrt{481}};z=9\cdot\dfrac{-1}{\sqrt{481}}=\dfrac{-9}{\sqrt{481}}\)