a)Ta có tam giác ABC cân

=>:AB=AC;góc B=góc C.

Xét tam giác AMB và tam giác AMC có:

AB=AC(cmt)

góc BAM=góc CAM (AM là phân giác của góc A).

AM chung.

=>tam giác AMB = tam giác AMC(c-g-c)

b) Vì tam giác AMB = tam giác AMC

=>góc AMB=góc AMC (2 góc tương ứng)

Mà 2 góc ở vị trí kề bù => góc AMB=góc AMC=180:2=90độ

=>AM vuông góc BC

c)

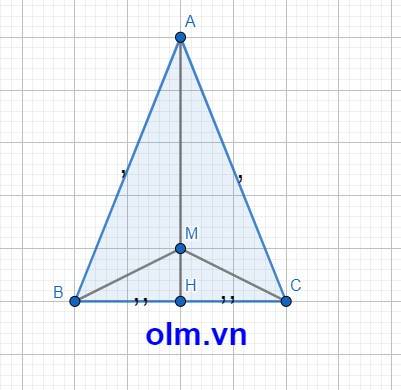
Nếu M là điểm tùy ý trên AH thì BM = MC chứ không phải BM = BA em nhé. 

@Nguyễn Thị Thương Hoài :vâng

Em cần viết đề bài bằng công thức toán học với biểu tượng Σ trên góc trái màn hình thì mọi người mới hiểu đúng đề để giúp em được.

                   2\(x\) = 3y ⇒  \(x\) = \(\dfrac{3}{2}\)y

                    4y = 5z ⇒ z = \(\dfrac{4}{5}y\)

               Thay \(x=\dfrac{3}{2}y;\)  z = \(\dfrac{4}{5}y\)  vào \(x+y+z\) = 11 ta có:

                        \(\dfrac{3}{2}y\) + y + \(\dfrac{4}{5}y\) = 11

                           \(\dfrac{33}{10}\)y           = 11

                               y            = 11 : \(\dfrac{33}{10}\)

                              y             = \(\dfrac{10}{3}\)

                               \(x\) = \(\dfrac{3}{2}\) x \(\dfrac{10}{3}\) = 5

                               z = \(\dfrac{4}{5}\) x \(\dfrac{10}{3}\) = \(\dfrac{8}{3}\)

Vậy \(\left(x;y;z\right)\) = (5; \(\dfrac{10}{3}\); \(\dfrac{8}{3}\)) 

a: Xét ΔABC có \(\widehat{B}>\widehat{C}\)

mà AC,AB lần lượt là cạnh đối diện của các góc ABC,ACB

nên AC>AB

b: ΔAHB vuông tại H

=>AB là cạnh lớn nhất trong ΔAHB

=>AB>AH

c: Xét ΔMAB và ΔMEC có

MA=ME

\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔMAB=ΔMEC
d: BC=24cm

=>\(CM=\dfrac{BC}{2}=12\left(cm\right)\)

Xét ΔCAE có

G là trọng tâm

CM là đường trung tuyến

Do đó: \(CG=\dfrac{2}{3}CM=\dfrac{2}{3}\cdot12=8\left(cm\right)\)

a,có x,y là 2 đại lg tln=>y=a/x(1)

thay x=2,y=-3 ta có: -3=a/2

=>a=-6

a;         Vì \(x;y\) là hai đại lượng tỉ lệ nghịch 

              nên a = \(x.y\) = 2.-3 = -6

  b;       \(x_1\)    = \(\dfrac{a}{y_1}\)      = \(\dfrac{-6}{6}\) = -1

            y₂ = y₁ - 15 = 6 - 15 = -9

            \(x_2\)   = \(\dfrac{a}{y_2}\) = \(\dfrac{-6}{-9}\) = \(\dfrac{2}{3}\)

4\(x\) = 3y = 2z 

\(x=\dfrac{3y}{4}\); z = \(\dfrac{3y}{2}\)

Thay \(x=\dfrac{3y}{4};z=\dfrac{3y}{2}\) vào biểu thức \(x+y+z\) = 65

Ta có: \(\dfrac{3y}{4}+y+\dfrac{3y}{2}=65\)

          y.(\(\dfrac{3}{4}+1+\dfrac{3}{2}\)) = 65

        y.\(\dfrac{13}{4}\) = 65

       y = 65 : \(\dfrac{13}{4}\)

       y = 20 

\(x\) = 20 x \(\dfrac{3}{4}\) = 15

z = 20 x \(\dfrac{3}{2}\) = 30

Vậy (\(x;y;z\)) = (15; 20; 30)

Lời giải:

Áp dụng TCDTSBN:

$4x=3y=2z=\frac{x}{\frac{1}{4}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{2}}=\frac{x+y+z}{\frac{1}{4}+\frac{1}{3}+\frac{1}{2}}=\frac{65}{\frac{13}{12}}=60$

$\Rightarrow x=60:4=15; y=60:3=20; z=60:2=30$

Lời giải:

Đặt $\frac{x}{-2}=\frac{y}{3}=k\Rightarrow x=-2k; y=3k$. Khi đó:

$x^2-y^2=-45$

$\Rightarrow (-2k)^2-(3k)^2=-45$

$\Rightarrow -5k^2=-45\Rightarrow k^2=9\Rightarrow k=\pm 3$
Với $k=3$ thì:

$x=-2k=-6; y=3k=9$

Với $k=-3$ thì:

$x=-2k=6; y=3k=-9$

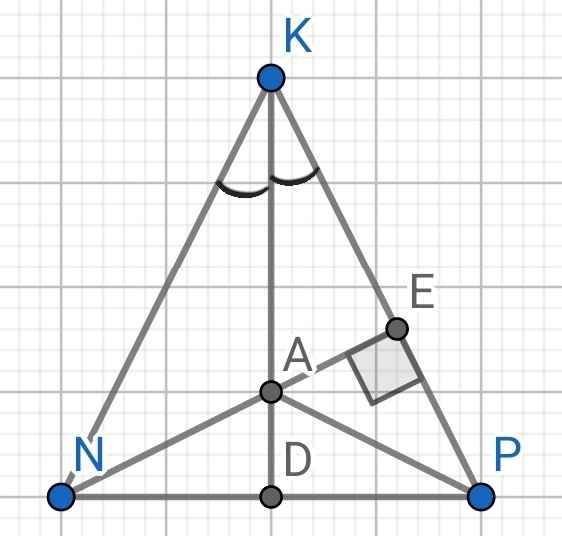
a) Do KD là tia phân giác của ∠NKP (gt)

⇒ ∠NKD = ∠PKD

Do ∆KNP cân tại K (gt)

⇒ KN = KP

Xét ∆KND và ∆KPD có:

KN = KP (cmt)

∠NKD = ∠PKD (cmt)

KD là cạnh chung

⇒ ∆KND = ∆KPD (c-g-c)

b) ∆KNP cân tại K (gt)

KD là đường phân giác (gt)

⇒ KD cũng là đường trung tuyến của ∆KNP

c) ∆KNP cân tại K (gt)

KD là đường trung tuyến (cmt)

⇒ KD cũng là đường cao của ∆KNP

Lại có:

NE ⊥ KP (gt)

⇒ NE là đường cao thứ hai của ∆KNP

⇒ A là giao điểm của hai đường cao AD và NE của ∆KNP

⇒ PA là đường cao thứ ba của ∆KNP

⇒ PA ⊥ KN

Gọi O là giao điểm của AE và BI. 
Do I là trung điểm của AC nên AI = IC. 
Gọi H là hình chiếu của I lên BC. 
Do HI vuông góc với BC nên tam giác BHI và CHI là các tam giác vuông cân tại I.
Trong tam giác BHI, ta có $$BH^2 + IH^2 = BI^2$$.
Trong tam giác CHI, ta có $$CH^2 + IH^2 = CI^2$$.
Cộng ta được $$BH^2 + CH^2 + 2IH^2 = BI^2 + CI^2$$.
Nhưng $$BH + CH = BC$$ và $$BI^2 + CI^2 = BC^2$$ (do tam giác BIC là tam giác vuông tại I), nên ta có $$BC^2 + 2IH^2 = BC^2$$.
Điều này chỉ ra rằng $$IH = 0$$, tức là I trùng với H.
Do I trùng với H, điểm I nằm trên BC. Vì vậy, đường thẳng AE (đường thẳng vuông góc với BC tại E) sẽ vuông góc với BI tại I.
Vậy AE vuông góc với BI. 

Gọi \(F\) là giao điểm của \(AB\) và \(EI\)
Xét \(\Delta IAF\) và \(\Delta ICE\)
có: \(\widehat{IAF}=\widehat{ICE}=90^o\left(gt\right)\)
      \(IA=IC\left(gt\right)\)
      \(\widehat{AIF}=\widehat{CIE}\) (đối đỉnh)
\(\Rightarrow\Delta IAF=\Delta ICE\left(g-c-g\right)\)
\(\Rightarrow IF=IE\) (hai cạnh tương ứng)
Xét tứ giác \(AFCE\)
có: \(IA=IC\left(gt\right)\)
      \(IF=IE\left(cmt\right)\)
\(\Rightarrow\) Tứ giác \(AFCE\) là hình bình hành
\(\Rightarrow AE//FC\left(1\right)\)
Xét \(\Delta BFC\)
có: \(CI\perp BF\left(gt\right)\)
      \(FI\perp BC\left(gt\right)\)
\(\Rightarrow I\) là trực tâm của \(\Delta BFC\)
\(\Rightarrow BI\perp FC\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow AE\perp BI\left(đpcm\right)\)