Cho parabol (P): y =\(\dfrac{1}{2}\)\(x^2\)
x2 và đường thẳng (d): y = mx -\(\dfrac{1}{2}\)m2 + m + 1
a. Với m = 1, xác định toạ độ các giao điểm A, B của (d) và (P);
b. Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao
cho |x1 - x2| = 2.
Bài 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
$M.\frac{1}{2}=\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{210}+\frac{1}{240}$
$=\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{14.15}+\frac{1}{15.16}$
$=\frac{5-4}{4.5}+\frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{15-14}{14.15}+\frac{16-15}{15.16}$
$=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{14}-\frac{1}{15}+\frac{1}{15}-\frac{1}{16}$
$=\frac{1}{4}-\frac{1}{16}=\frac{3}{16}$
$\Rightarrow M=\frac{3}{8}$
Vì $\frac{1}{3}< \frac{3}{8}< \frac{1}{2}$ nên $\frac{1}{3}< M< \frac{1}{2}$
M=1/10 + 1/15 + 1/21 + 1/28 +....+ 1/105 + 1/120 M=1/2*5 + 1/5*3 +1/3*7 + 1/7*4 +....+ 1/7*15 + 1/15*8 M=2(1/2*2*5+1/2*5*3+1/2*3*7+1/2*7*4+....+1/2*7*15+1/2*15*8) M=2(1/4*5+1/5*6+1/6*7+1/7*8+....+1/14*15+1/15*16) M=2(1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8+....+1/14-1/15+1/15-1/16) M=2(1/4-1/16) M=2(4/16-1/16) M=2*3/16 M=3/8


They are at the zoo because they want to see the animals
15 . => They are at the zoo because they want to see the animals .

Bài 1:
\(E=\frac{1}{6}+\frac{1}{66}+\frac{1}{176}+...+\frac{1}{9894}\\ =\frac{1}{1.6}+\frac{1}{6.11}+\frac{1}{11.16}+...+\frac{1}{97.102}\)
\(\Rightarrow 5E=\frac{6-1}{1.6}+\frac{11-6}{6.11}+\frac{16-11}{11.16}+...+\frac{102-97}{97.102}\\ =1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+\frac{1}{11}-\frac{1}{16}+...+\frac{1}{97}-\frac{1}{102}\\ =1-\frac{1}{102}=\frac{101}{102}\\ \Rightarrow E=\frac{101}{102}:5=\frac{101}{510}\)
Bài 2:
Gọi số học sinh cả lớp là $a$
Số học sinh vắng mặt ban đầu: $\frac{a}{1+6}.1=\frac{a}{7}$ (hs)
Sau khi 2 học sinh ra khỏi lớp thì lớp còn $a-2$ hs
Số hs vắng mặt lúc sau: $\frac{a-2}{1+4}.1=\frac{a-2}{5}$ (hs)
Có:
$\frac{a-2}{5}=\frac{a}{7}+2=\frac{a+14}{7}$
$\Rightarrow 7(a-2)=5(a+14)$
$\Rightarrow 7a-14=5a+70$
$\Rightarrow 2a=84$
$\Rightarrow a=42$ (hs)

Lời giải:
15 phút ~ 0,25 giờ người đó đi được 1000 m ~ 1 km
Trong 1 giờ người đó đi được:
$1:0,25=4$ (km)
Vậy tốc độ người đó đi là 4km/h
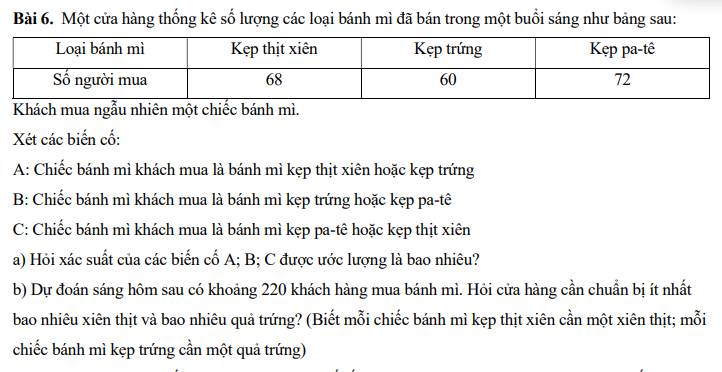



a) Với m = 1, ta có:
⇒ (d): y = x - 1/2 + 2 = x + 3/2
Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = x + 3/2
⇔ x² = 2x + 3
⇔ x² - 2x - 3 = 0
Do a - b + c = 1 - (-2) + 3 = 0 nên phương trình có hai nghiệm:
x₁ = -1; x₂ = -c/a = 3
x₁ = -1 ⇒ y = 1/2 . (-1)² = 1/2
⇒ A(-1; 1/2)
x₂ = 3 ⇒ y = 1/2 . 3² = 9/2
⇒ B(3; 9/2)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = mx - 1/2 m² + m + 1
⇔ x² = 2mx - m² + 2m + 2
⇔ x² - 2mx + m² - 2m - 2
∆' = (-m)² - 1.(m² - 2m - 2)
= m² - m² + 2m + 2
= 2m + 2
Để phương trình có hai nghiệm phân biệt thì ∆' > 0
⇔ 2m + 2 > 0
⇔ 2m > -2
⇔ m > -1
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = 2m
x₁x₂ = m² - 2m - 2
Ta có:
|x₁ - x₂| = (x₁ - x₂)² = [(x₁ + x₂)² - 4x₁x₂]
= [(2m)² - 4.(m² - 2m - 2)]
= (4m² - 4m² + 8m + 4)
= 8m + 4
= 2(2m + 2)
Mà |x₁ - x₂| = 2
⇔ 2(2m + 2) = 2
⇔ (2m + 2) = 1
⇔ 2m + 2 = 1
⇔ 2m = -1
⇔ m = -1/2 (nhận)
Vậy m = -1/2 thì phương trình có hai nghiệm phân biệt thỏa mãn |x₁ - x₂| = 2