P=(1+a/bc)(1+b/c+a)(1+c/a+b)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chọn 3 em nam và 2 em nữ có \(C_{50}^2\cdot C_{50}^3\) cách
\(\Rightarrow P=\dfrac{C^3_{30}\cdot C_{20}^2}{C^5_{50}}=\dfrac{2755}{7567}\)
b) TH1: 5 em nam có \(C^5_{30}\) cách
TH2: 4 em nam và 1 em nữ có: \(C^4_{30}\cdot C^1_{20}\) cách
TH3: 3 em nam và 2 em nữ có: \(C^3_{30}\cdot C_{20}^2\) cách
TH4: 2 em nam và 3 em nữ có: \(C^2_{30}\cdot C_{20}^3\) cách
TH5: 1 em nam và 4 em nữ có: \(C^1_{30}\cdot C^4_{20}\) cách
Xác xuất: \(P=\dfrac{C^5_{30}+C_{30}^4\cdot C_{20}^1+C^3_{30}\cdot C^2_{20}+C^2_{30}\cdot C^3_{20}+C^1_{30}\cdot C^4_{20}}{C^5_{50}}=\dfrac{262907}{264845}\)
c) TH1: 4 em nam và 1 em nữ có \(C^4_{30}\cdot C^1_{20}\) cách
TH2: 3 em nam và 2 em nữ có \(C^3_{30}\cdot C^2_{20}\) cách
TH3: 2 em nam và 3 em nữ có \(C^2_{30}\cdot C^3_{20}\) cách
TH4: 1 em nam và 4 em nữ có \(C^1_{30}\cdot C^4_{20}\) cách
Xác xuất: \(P=\dfrac{C_{30}^4\cdot C_{20}^1+C^3_{30}\cdot C^2_{20}+C^2_{30}\cdot C^3_{20}+C^1_{30}\cdot C^4_{20}}{C^5_{50}}=\dfrac{8525}{9212}\)

Đây là dạng toán nâng cao chuyên đề toán hiệu tỉ, ẩn hiệu, cấu trúc đề thi chuyên, hsg, violympic. Hôm nay olm sẽ hướng dẫn các em làm dạng này như sau.
Coi số bò sau khi bán đi 7 con là 1 phần thì ta có sơ đồ:
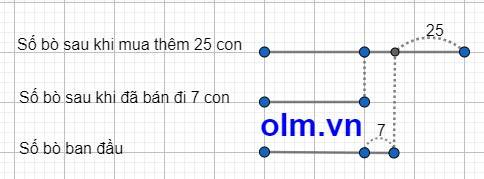
Theo sơ đồ ta có: Số bò ban đầu là: (25 + 7) : (2 - 1) + 7 = 39 (con)
Đáp số: 39 con
Thử lại ta có: Số bò sau khi mua thêm 25 con là: 39 + 25 = 64 (con)
Số bò sau khi bán đi 7 con là: 39 - 7 = 32 (con)
Nếu mua thêm 25 con thì số bò khi đó gấp số bò ban đầu sau khi bán đi 7 con là:
64: 32 = 2 (ok nha em)
Đây là dạng toán nâng cao chuyên đề hiệu tỉ, ẩn tỉ. Cấu trúc thi chuyên, thi hsg, thi viloympic. Hôm nay olm sẽ hướng dẫn em giải dạng này bằng sơ đồ đoạn thẳng như sau.
Coi số bò sau khi bán đi 7 con là 1 phần thì ta có sơ đồ:
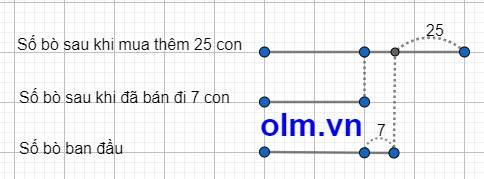
Theo sơ đồ ta có: Số bò ban đâu là: (25 + 7) : (2 - 1) + 7 = 39 (con)
Đáp số : 39 con bò.
Thử lại ta có: Số bò sau khi bán đi 7 con là: 39- 7 = 32 (con)
Số bò sau khi mua thêm 25 con là: 39 + 25 = 64 (con)
Số bò sau khi mua thêm so với số bò sau khi bán đi gấp số lần là:
64 : 32 = 2 (ok) em nhé. Vậy đáp số là đúng!

Khi viết chữ số 3 vào bên trái số tự nhiên hai chữ số thì số mới hơn số cần tìm 300 đơn vị
Hiệu số phần bằng nhau: 7-1=6(phần)
Số ban đầu là: 300 : 6 x 1 = 50
Đáp số: số cần tìm là 50
Gọi số tự nhiên có 2chữ số ban đầu là \(\dfrac{ }{ab}\)(0 ≤a,b≤9;a,b∈N,a≠0)
Khi viết thêm chữ số 3 vào bân trái nó ta được số \(\dfrac{ }{3ab}\)
Ta có: \(\dfrac{ }{3ab}\) =300+\(\dfrac{ }{ab}\) =\(\overline{7ab}\) ⇔ \(\dfrac{ }{6ab}\) = 300 ⇔ \(\overline{ab}\) = 50
��¯,(0≤�,�≤9;�,�∈ℕ,�≠0

Khoảng cách 2 số liên tiếp: 40:(5-1)=10 (đơn vị)
Số ở giữa là: 200:5=40
Vậy số bé nhất là: 40 - 2 x 10 = 20
Đáp án++Giải thích các bước giải::
Gọi 55 số đó lần lượt là a;b;c;d;e�;�;�;�;�
Theo bài ra ,, ta có ::
e−a=40�-�=40
a+b+c+d+e�+�+�+�+�
→→ Số số hạng là :5(:5( đề cho ))
→→ Tổng là :(a+e)×5:2=200:(�+�)×5:2=200
→(a+e)×5=200×2=400→(�+�)×5=200×2=400
→a+e=400:5=80→�+�=400:5=80 *
Vì :e−a=40:�-�=40
→e=40+a→�=40+�
Thay e=40+a�=40+� vào * ,, ta có ::
→a+40+a=80→�+40+�=80
→2×a=80−40=40→2×�=80-40=40
→a=40:2=20→�=40:2=20
Vậy :: số bé nhất là 20

a) (x - 3)¹⁰ + (y² - 4)¹⁰ = 0 (1)
Do (x - 3)¹⁰ 0 và (y² - 4)¹⁰ 0 với mọi x, y R
(1) (x - 3)¹⁰ = 0 và (y² - 4)¹⁰ = 0
*) (x - 3)¹⁰ = 0
x - 3 = 0
x = 3
*) (y² - 4)¹⁰ = 0
y² - 4 = 0
y² = 4
y = -2; y = 2
Vậy ta được các cặp (x: y) thỏa mãn:
(3; -2); (3; 2)
b) xy + 5x = 2y + 13
xy + 5x - 2y = 13
(xy + 5x) - 2y = 13
x(y + 5) - 2y - 10 = 13 - 10
x(y + 5) - 2(y + 5) = 3
(x - 2)(y + 5) = 3
*) TH1: x - 2 = -3; y + 5 = -1
+) x - 2 = -3
x = -3 + 2
x = - 1
+) y + 5 = -1
y = -1 - 5
y = -6
*) TH2: x - 2 = -1; y + 5 = -3
+) x - 2 = -1
x = -1 + 2
x = 1
+) y + 5 = -3
y = -3 - 5
y = -8
*) TH3: x - 2 = 1; y + 5 = 3
+) x - 2 = 1
x = 1 + 2
x = 3
+) y + 5 = 3
y = 3 - 5
y = -2
*) TH4: x - 2 = 3; y + 5 = 1
+) x - 2 = 3
x = 3 + 2
x = 5
+) y + 5 = 1
y = 1 - 5
y = -4
Vậy ta tìm được câc cặp giá trị (x; y) thỏa mãn:
(5; -4); (3; -2); (1; -8); (-1; -6)

\(6xy-10x+3y=12\)
\(\Leftrightarrow6xy+3y-10x-5=7\)
\(\Rightarrow3y\left(2x+1\right)-5\left(2x+1\right)=7\)
\(\Leftrightarrow\left(2x+1\right)\left(3y-5\right)=7\)
Ta có bảng:
| 2x+1 | -7 | -1 | 1 | 7 |
| 3y-5 | -1 | -7 | 7 | 1 |
| x | -4 | -1 | 0 | 3 |
| y | 4/3 (loại) | -2/3 (loại) | 4 | 2 |
Vậy \(\left(x;y\right)=\left(0;4\right);\left(3;2\right)\)

\(x^2\left(x-5\right)-4\left(5-x\right)=0\)
\(\Leftrightarrow x^2\left(x-5\right)+4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x^2+4\right)\left(x-5\right)=0\)
\(\Rightarrow x-5=0\) (vì \(x^2+4>0\forall x\))
\(\Leftrightarrow x=5\)
`x^2(x-5)-4(5-x)=0`
\(\Leftrightarrow x^2\left(x-5\right)+4\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(x^2+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x^2+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x^2=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x\in\varnothing\end{matrix}\right.\)

Yêu cầu của đề là gì vậy ?