Tích của hai số là 2165. Nếu gấp thừa số thứ nhất lên 3 lần giữ nguyên thừa số thứ hai thì tích hai số là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
a. Để $M$ là phân số thì $n-3\neq 0$ hay $n\neq 3$
b. $n=0$ thì $M=\frac{4}{0-3}=\frac{-4}{3}$
$n=9$ thì $M=\frac{4}{9-3}=\frac{2}{3}$
$n=-9$ thì $M=\frac{4}{-9-3}=\frac{-1}{3}$
Bài 9:
\(\frac{13}{25}=\frac{26}{50}=\frac{39}{75}\)

1.
Trung bình cộng của 2 đáy là:
\(40:2=20\left(dm\right)\)
Diện tích hình thang đó là:
\(20\times10=200\left(dm^2\right)\)
2.
Tổng độ dài 2 đáy là:
\(13,7\times2=27,4\left(m\right)\)
Diện tích hình thang đó là:
\(27,4\times1,7:2=23,29\left(m^2\right)\)
3.
Chiều cao của hình thang đó là:
\(\dfrac{4}{15}\times2:\dfrac{2}{3}=\dfrac{24}{30}=\dfrac{4}{5}\left(m\right)\)
Trung bình cộng của 2 đáy là:
\(\dfrac{2}{3}:2=\dfrac{2}{3}\times\dfrac{1}{2}=\dfrac{2}{6}=\dfrac{1}{3}\left(m\right)\)

Lời giải:
Xét tam giác $CEK$ và $AED$ có:
$\widehat{A_1}=\widehat{C_1}$ (2 góc so le trong)
$\widehat{E_1}=\widehat{E_2}$ (đối đỉnh)
$AE=EC$ (do $E$ là trung điểm $AC$)
$\Rightarrow \triangle CEK=\triangle AED$ (g.c.g)
$\Rightarrow CK=AD$
Mà $AD=BD$ (do $D$ là trung điểm $AB$)
$\Rightarrow CK=BD$
-----------------------
Từ tam giác bằng nhau vừa cm suy ra $EK=ED$
$\Rightarrow DE=\frac{1}{2}DK(1)$
Lại có:
Xét tam giác $BDC$ và $KCD$ có:
$\widehat{BDC}=\widehat{KCD}$ (so le trong)
$DC$ chung
$BD=CK$ (cmt)
$\Rightarrow \triangle BDC=\triangle KCD$ (c.g.c)
$\Rightarrow BC=KD(2)$
Từ $(1); (2)\Rightarrow DE=\frac{1}{2}BC$

Đổi \(12\) tạ đường = \(1200kg\) đường.
Ngày đầu cửa hàng đó bán được:
\(\left(1200-18\right):2=591\left(kg\right)\)
Ngày sau cửa hàng đó bán được:
\(1200-591=609\left(kg\right)\)
Đáp số: Ngày đầu: \(591kg\)
Ngày sau: \(609kg\)
12 tạ
12 tạ =1200kg
ngày sau bán được số kg là
[1200+18] ;2=609 [kg]
ngày thứ nhất có số kg là
1200-609=591[kg]
đáp số 591kg

\(205:x-90:x=23\)
\(\left(205-90\right):x=23\)
\(115:x=23\)
\(x=115:23\)
\(x=5\)
205 : X - 90 : X = 23
(205 - 90 ) : X = 23
115 : X = 23
X = 115 : 23
X = 5
Nhớ tick nha!

Để phân số \(\dfrac{12}{3x-1}\) mang giá trị nguyên
Khi \(12⋮3x-1\) hay \(3x-1\inƯ12=\left\{-12;-6;-4;-3;-2;-1;1;2;3;4;6;12\right\}\)
\(\Rightarrow x=\left\{-1;0;1\right\}\)
\(\dfrac{12}{3x-1}\inℤ\)
\(\Rightarrow3x-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
\(\Rightarrow3x\in\left\{2;0;3;-1;4;-2;5;-3;7;-5;13;-11\right\}\)
\(\Rightarrow x\in\dfrac{2}{3};\dfrac{0}{1};\dfrac{4}{3};-\dfrac{2}{3};\dfrac{5}{3};-1;\dfrac{7}{3};-\dfrac{5}{3};\dfrac{13}{3};-\dfrac{11}{3}\)
Mà \(x\inℤ\)
Vậy \(x\in\left\{0;1;-1\right\}\)
Vậy \(x\in\left\{1;-1;0\right\}\) để \(\dfrac{12}{3x-1}\) nguyên


a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)

Số gạo của cửa hàng đó mà buổi chiều bán được là:
\(243:3=81\left(kg\right)\)
Cả 2 buổi cửa hàng đó bán được số gạo là:
\(243+81=324\left(kg\right)\)
Đáp số: \(324kg\)
Số gạo buổi chiều bán được là:
\(243\div3=81\left(kg\right)\)
Cả hai buổi bán được số kg gạo là:
\(243+81=324\left(kg\right)\)
Đáp số: \(324kg\) gạo
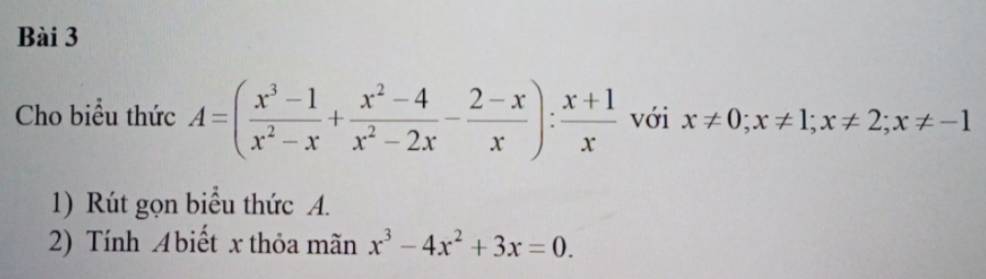
Nếu giữ nguyên thừa số thứ hai và gấp thừa số thứ nhất lên 3 lần thì tích hai số là:
2165 x 3 = 6495
Đs..
Giữ nguyên thừa số thứ hai và gấp thừa số thứ nhất lên 3 lần thì tích 2 số là:
\(2165\times3=6495\)
Đáp số: \(6495.\)