Bài 1:

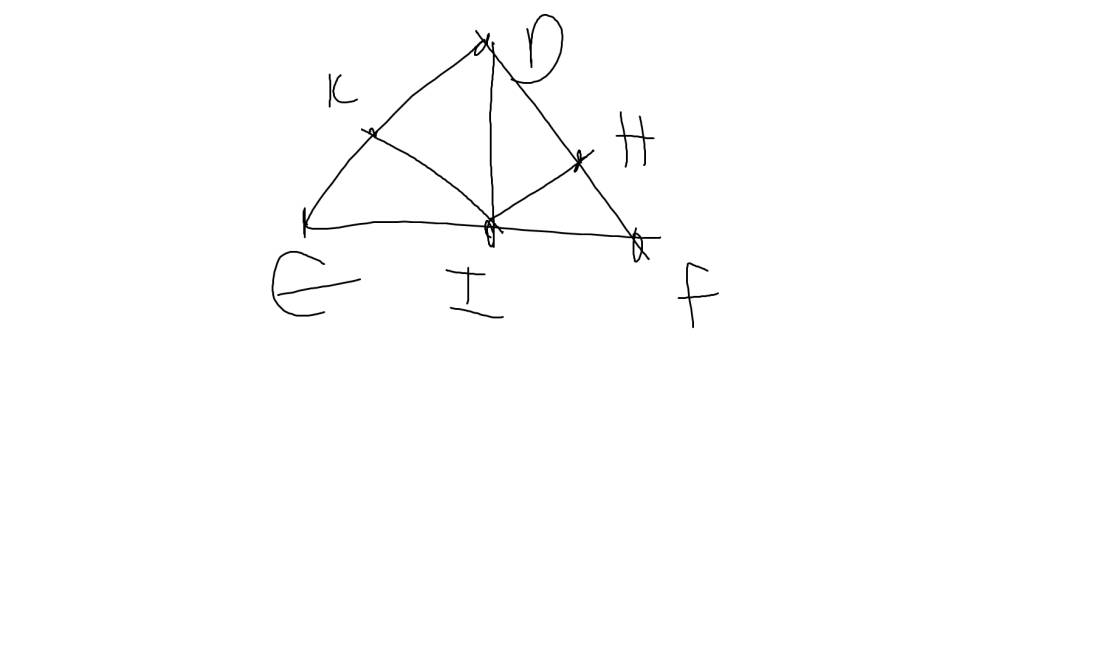
a: Xét ΔDEI và ΔDFI có

DE=DF

EI=FI

DI chung

Do đó: ΔDEI=ΔDFI

b: Ta có: ΔDEI=ΔDFI

=>\(\widehat{DIE}=\widehat{DIF}\)

mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)

nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)

=>DI\(\perp\)EF

ΔDEI=ΔDFI

=>\(\widehat{EDI}=\widehat{FDI}\)

=>DI là phân giác của góc EDF

c: Xét ΔIKE vuông tại K và ΔIHF vuông tại H có

IE=IF

\(\widehat{IEK}=\widehat{IFH}\)

Do đó: ΔIKE=ΔIHF

d: ta có: ΔIKE=ΔIHF

=>KE=HF và IK=IH

Ta có: DK+KE=DE

DH+HF=DF

mà DE=DF và KE=HF

nên DK=DH

=>D nằm trên đường trung trực của HK(1)

Ta có: IK=IH

=>I nằm trên đường trung trực của HK(2)

Từ (1),(2) suy ra DI là đường trung trực của HK

=>DI\(\perp\)HK

Xét ΔDEF có \(\dfrac{DK}{DE}=\dfrac{DH}{DF}\)

nên KH//EF

Bài 2:

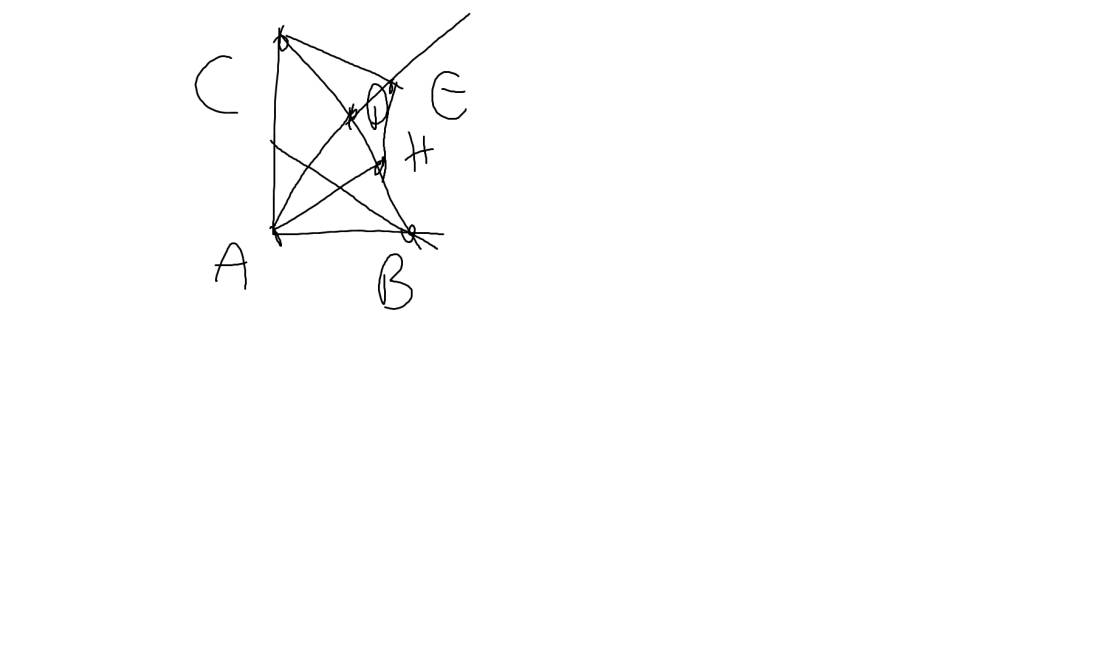
a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-30^0=60^0\)

Xét ΔABD có

AH là đường cao

AH là đường trung tuyến

Do đó: ΔABD cân tại A

Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)

nên ΔABD đều

b: ΔABD đều

=>\(\widehat{BAD}=\widehat{BDA}=60^0\) và AB=BD=AD

\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)

=>\(\widehat{CAD}+60^0=90^0\)

=>\(\widehat{CAD}=30^0\)

Xét ΔDCA có \(\widehat{DCA}=\widehat{DAC}\)

nên ΔDAC cân tại D

=>DA=DC

c: Xét ΔDEC vuông tại E và ΔDHA vuông tại H có

DC=DA

\(\widehat{EDC}=\widehat{HDA}\)

Do đó: ΔDEC=ΔDHA

=>AH=CE và DE=DH

d: Xét ΔDEH và ΔDAC có

\(\dfrac{DE}{DA}=\dfrac{DH}{DC}\)

\(\widehat{EDH}=\widehat{ADC}\)

Do đó: ΔDEH~ΔDAC

=>\(\widehat{DEH}=\widehat{DAC}\)

=>EH//AC

a; \(\dfrac{8}{9}\) + \(\dfrac{2}{6}\)  > \(\dfrac{5}{9}\) = \(\dfrac{3}{9}\) + \(\dfrac{2}{9}\)

Vậy \(\dfrac{8}{9}\) + \(\dfrac{2}{6}\) > \(\dfrac{3}{9}\) + \(\dfrac{2}{9}\)

b; \(\dfrac{11}{14}\) > \(\dfrac{10}{14}\) = \(\dfrac{5}{7}\)  = \(\dfrac{3}{7}\) + \(\dfrac{2}{7}\)

Vậy \(\dfrac{11}{14}\) > \(\dfrac{3}{7}\) + \(\dfrac{2}{7}\)

Chu vi vườn hoa đó là:

\(7,5\times2\times3,14=47,1\left(m\right)\)

Số cây cần phải trồng là:

\(47,1:0,3=157\left(cây\right)\) 

- Những lợi ích kinh tế mà sóng, thủy triều và dòng biển đem tại cho chúng ta

+ Phát triển công nghiệp năng lượng, sản xuất điện năng.

+ Phát triển ngư nghiệp (đánh bắt hải sản).

+ Nghiên cứu khoa học, thủy văn, quân sự,…

- Tại Việt Nam, con người đã biết sử dụng thủy triều để phục vụ

+ Công nghiệp: Sản xuất điện (năng lượng sóng, thủy triều).

+ Ngư nghiệp: Đánh bắt hải sản (ngư trường thủy sản).

+ Nghiên cứu khoa học, thủy văn, quân sự,…

- Những lợi ích kinh tế mà sóng, thủy triều và dòng biển đem tại cho chúng ta

+ Phát triển công nghiệp năng lượng, sản xuất điện năng.

+ Phát triển ngư nghiệp (đánh bắt hải sản).

+ Nghiên cứu khoa học, thủy văn, quân sự,…

- Tại Việt Nam, con người đã biết sử dụng thủy triều để phục vụ

+ Công nghiệp: Sản xuất điện (năng lượng sóng, thủy triều).

+ Ngư nghiệp: Đánh bắt hải sản (ngư trường thủy sản).

+ Nghiên cứu khoa học, thủy văn, quân sự,…

- Phát triển công nghiệp điện.

- Cung cấp nước tưới cho sản xuất.

- Làm muối.

- Là điều kiện thuận lợi cho tàu thuyền ra khơi.

- Là chiến thuật quân sự (trận đánh trên sông Bạch Đằng năm 938).

Lấy 28 viên bi nkaa

a, \(\dfrac{27}{45}+\dfrac{12}{30}=\dfrac{3}{5}+\dfrac{2}{5}=\dfrac{5}{5}=1\)

b, \(\dfrac{6}{18}+\dfrac{1}{3}=\dfrac{1}{3}+\dfrac{1}{3}=\dfrac{2}{3}\)

a) 27/45 + 12/30

= 3/5 + 2/5

= 5/5 =1.

b) 6/18 + 1/3

=1/3 + 1/3

= 2/3.