Tìm các số x,y,z biết \(\frac{x}{2}\)=\(\frac{y}{3}\)=\(\frac{z}{4}\) và \(^{x^2}\)-\(^{y^2}\)+\(^{z^2}\)=44
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



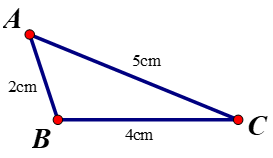
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
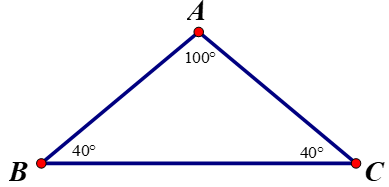
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
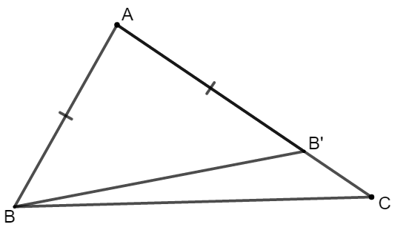
7)
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C

tổng số tuổi của 40 thầy cô là 1684 tuổi
sang năm học mới thì tổng số tuổi của 40-2+2 = 40 thầy cô giáo là
1684 - 60 - 55 + 21 + 22 = 1526
tuổi trung bình các thầy cô trong năm mới là 1526/40 = 38,15 tuổi

x = -2 ; x = -3 mới là nghiệm được chứ em :))
P(x) = x2 + 5x + 6
= x2 + 2x + 3x + 6
= ( x2 + 2x ) + ( 3x + 6 )
= x( x + 2 ) + 3( x + 2 )
= ( x + 2 )( x + 3 )
P(x) = 0 <=> ( x + 2 )( x + 3 ) = 0
<=> x + 2 = 0 hoặc x + 3 = 0
<=> x = -2 hoặc x = -3
Vậy ...

f(x) = 2x2 + x - 3
= 2x2 - 2x + 3x - 3
= ( 2x2 - 2x ) + ( 3x - 3 )
= 2x( x - 1 ) + 3( x - 1 )
= ( x - 1 )( 2x + 3 )
f(x) = 0 <=> ( x - 1 )( 2x + 3 ) = 0
<=> x - 1 = 0 hoặc 2x + 3 = 0
<=> x = 1 hoặc x = -3/2
Vậy x = 1 ; x = -3/2 là nghiệm của đa thức ( đpcm )

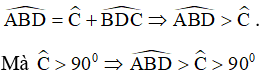
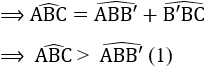
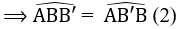
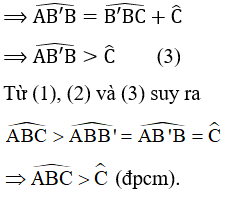
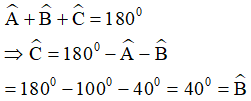
Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k\Rightarrow\hept{\begin{cases}x=2k\\y=3k\\z=4k\end{cases}}\)
Khi đó : x2 - y2 + z2 = 44
<=> 4k2 - 9k2 + 16k2 = 44
<=> 11k2 = 44
<=> k2 = 4
<=> k = ±2
Với k = 2 => x = 4 ; y = 6 ; z = 8
Với k = -2 => x = -4 ; y = -6 ; z = -8