Chứng minh :\(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1}{3^2}< \dfrac{1}{1\cdot3}=1-\dfrac{1}{3}\)
\(\dfrac{1}{5^2}< \dfrac{1}{3\cdot5}=\dfrac{1}{3}-\dfrac{1}{5}\)
...
\(\dfrac{1}{99^2}< \dfrac{1}{97\cdot99}=\dfrac{1}{97}-\dfrac{1}{99}\)
Do đó: \(\dfrac{1}{3^2}+\dfrac{1}{5^2}+...+\dfrac{1}{99^2}< 1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\)
=>\(B=1+\dfrac{1}{3^2}+\dfrac{1}{5^2}+...+\dfrac{1}{9^2}< 1+1=2\)
=>1<B<2
=>B không là số tự nhiên

a, 2/3 + 1/3 : x = 3/5
1/3 : x = -1/15
x = -1/45
b, x - 5/9 = -2/3
x = -1/9


\(A=1+\dfrac{1}{8}+\dfrac{1}{24}+\dfrac{1}{48}+\dfrac{1}{80}+\dfrac{1}{120}\)
\(A=\dfrac{1}{2.4}+\dfrac{1}{4.6}+\dfrac{1}{6.8}+\dfrac{1}{8.10}+\dfrac{1}{10.12}\)
\(2A=\dfrac{2}{2.4}+\dfrac{2}{4.6}+\dfrac{2}{6.8}+\dfrac{2}{8.10}+\dfrac{2}{10.12}\)
\(2A=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{12}\)
\(2A=1-\dfrac{1}{12}\)
\(2A=\dfrac{11}{12}\)
\(A=\dfrac{11}{12}:2=\dfrac{11}{24}\)
\(A=1+\dfrac{1}{8}+\dfrac{1}{24}+\dfrac{1}{48}+\dfrac{1}{80}+\dfrac{1}{120}\)
\(=1+\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+\dfrac{1}{8\cdot10}+\dfrac{1}{10\cdot12}\)
\(=1+\dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{10\cdot12}\right)\)
\(=1+\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{12}\right)\)
\(=1+\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{12}\right)=1+\dfrac{1}{2}\cdot\dfrac{5}{12}=1+\dfrac{5}{24}=\dfrac{29}{24}\)

\(B=\dfrac{1}{29}+\dfrac{2}{28}+...+\dfrac{28}{2}+\dfrac{29}{1}\)
\(=\left(\dfrac{1}{29}+1\right)+\left(\dfrac{2}{28}+1\right)+...+\left(\dfrac{28}{2}+1\right)+1\)
\(=\dfrac{30}{29}+\dfrac{30}{28}+...+\dfrac{30}{2}+\dfrac{30}{30}\)
\(=30\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{30}\right)=30A\)
=>\(\dfrac{A}{B}=\dfrac{1}{30}\)

\(A=1+\dfrac{1}{1+2}+...+\dfrac{1}{1+2+...+8}\)
\(=\dfrac{2}{2}+\dfrac{1}{2\cdot\dfrac{3}{2}}+...+\dfrac{1}{8\cdot\dfrac{9}{2}}\)
\(=\dfrac{2}{1\cdot2}+\dfrac{2}{2\cdot3}+...+\dfrac{2}{8\cdot9}\)
\(=2\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{8\cdot9}\right)\)
\(=2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)\)
\(=2\left(1-\dfrac{1}{9}\right)=2\cdot\dfrac{8}{9}=\dfrac{16}{9}\)

file:///C:/Users/Admin/Downloads/MicrosoftWindows.Client.CBS_cw5n1h2txyewy!InputApp/GraduationHappyGIF.gif
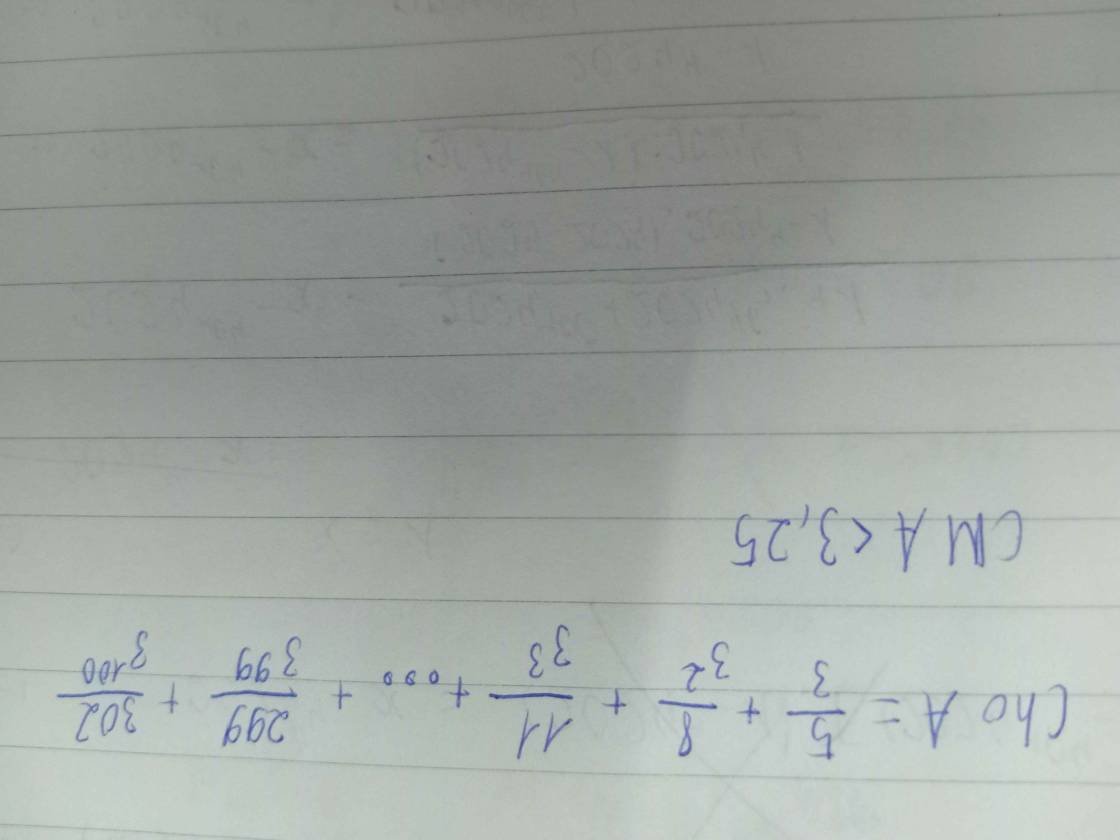
\(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\\ =\dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}\)
Ta có: \(\dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}< \dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{99.100}\\ \dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}< \dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ \dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}< \dfrac{1}{2}-\dfrac{1}{100}\\ \dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}< \dfrac{49}{100}< \dfrac{50}{100}=\dfrac{1}{2}\)
Hay \(\dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}< \dfrac{1}{2}\)
Vì \(\dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+\dfrac{1}{6.6}+...+\dfrac{1}{100.100}=\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
Vậy biểu thức \(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\)
1/3² + 1/4² + 1/5² + 1/6² + ... + 1/100²
< 1/(2.3) + 1/(3.4) + 1/(4.5) + 1/(5.6) + ... + 1/(99.100)
= 1/2 - 1/3 + 1/3 - 1/4 + 1/4 - 1/5 + 1/5 - 1/6 + ... + 1/99 - 1/100
= 1/2 - 1/100 < 1/2