
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
mà AB,AC,BC lần lượt là cạnh đối diện của các góc ACB,ABC,BAC
nên AB<AC<BC
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
c: ΔBAE=ΔBHE
=>BA=BH
Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
\(\widehat{HBK}\) chung
Do đó: ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
Xét ΔBKC cân tại B có \(\widehat{KBC}=60^0\)
nên ΔBKC đều

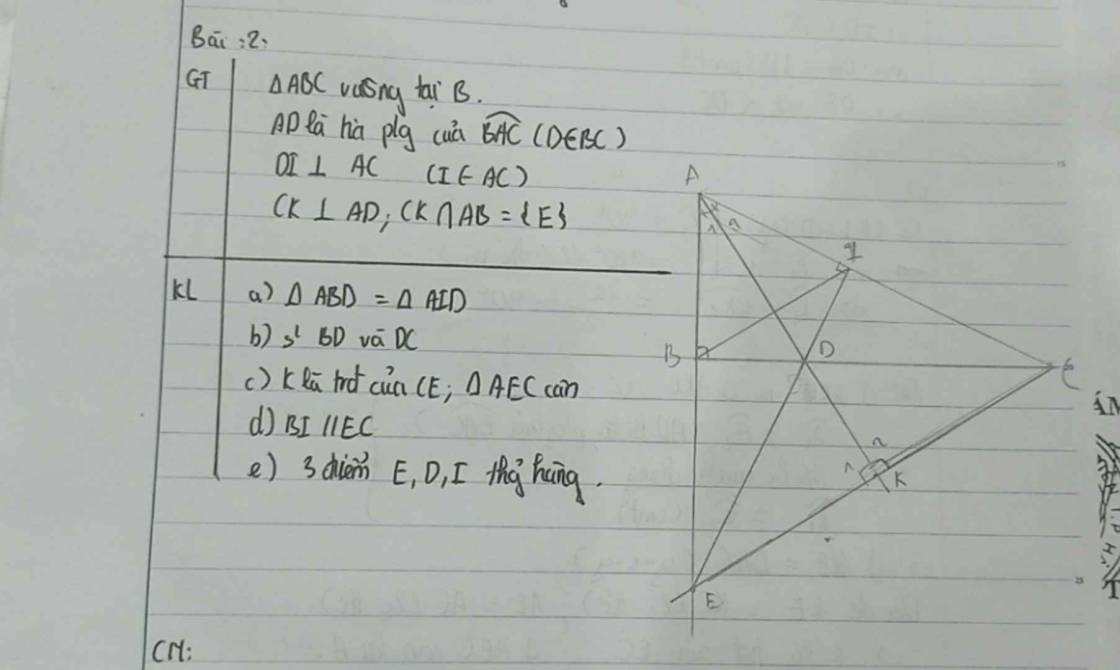
a: Xét ΔABD vuông tại B và ΔAID vuông tại I có
AD chung
\(\widehat{BAD}=\widehat{IAD}\)
Do đó: ΔABD=ΔAID
b: ta có: ΔABD=ΔAID
=>DB=DI
mà DI<DC(ΔDIC vuông tại I)
nên DB<DC
c: Xét ΔAEC có
AK là đường cao
AK là đường phân giác
Do đó: ΔAEC cân tại A
Ta có: ΔAEC cân tại A
mà AK là đường cao
nên K là trung điểm của EC
d: Xét ΔAEC có \(\dfrac{AB}{AE}=\dfrac{AI}{AC}\)
nên BI//EC
e: Xét ΔAEC có
AK,CB là các đường cao
AK cắt CB tại D
Do đó: D là trực tâm của ΔAEC
=>ED\(\perp\)AC
mà DI\(\perp\)AC
và ED,DI có điểm chung là D
nên E,D,I thẳng hàng

a: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
\(\widehat{MND}=\widehat{END}\)
Do đó: ΔNMD=ΔNED
b: Ta có; ΔNMD=ΔNED
=>DM=DE
Xét ΔDMF vuông tại M và ΔDEP vuông tại E có
DM=DE
\(\widehat{MDF}=\widehat{EDP}\)
Do đó: ΔDMF=ΔDEP
=>DF=DP
=>ΔDFP cân tại D
c: Ta có: ΔDMF=ΔDEP
=>MF=EP
ΔNMD=ΔNED
=>NM=NE
Ta có: NM+MF=NF
NE+EP=NP
mà NM=NE và MF=EP
nên NF=NP
=>N nằm trên đường trung trực của FP(1)
Ta có: DF=DP
=>D nằm trên đường trung trực của FP(2)
Ta có: KF=KP
=>K nằm trên đường trung trực của FP(3)
Từ (1),(2),(3) suy ra N,D,K thẳng hàng

g. \(-\dfrac{2}{3}\times\dfrac{4}{5}+\dfrac{1}{5}\div\dfrac{9}{11}=-\dfrac{8}{15}+\dfrac{1}{5}\times\dfrac{11}{9}=-\dfrac{8}{15}+\dfrac{11}{45}=\dfrac{24}{45}+\dfrac{11}{45}=\dfrac{35}{45}=\dfrac{7}{9}\)
h.
\(\left(-6,2\div2+3,7\right)\div0,2=\left(-3,1+3,7\right)\div0,2=0,6\div0,2=3\)
k.
\(\dfrac{2}{3}+\dfrac{1}{5}\times\dfrac{10}{7}=\dfrac{2}{3}+\dfrac{10}{35}=\dfrac{2}{3}+\dfrac{2}{7}=\dfrac{14}{21}+\dfrac{6}{21}=\dfrac{20}{21}\)
m.
\(\dfrac{2}{7}+\dfrac{5}{7}\times\dfrac{14}{25}=\dfrac{2}{7}+\dfrac{1\times2}{1\times5}=\dfrac{2}{7}+\dfrac{2}{5}=\dfrac{10}{35}+\dfrac{14}{35}=\dfrac{24}{35}\)

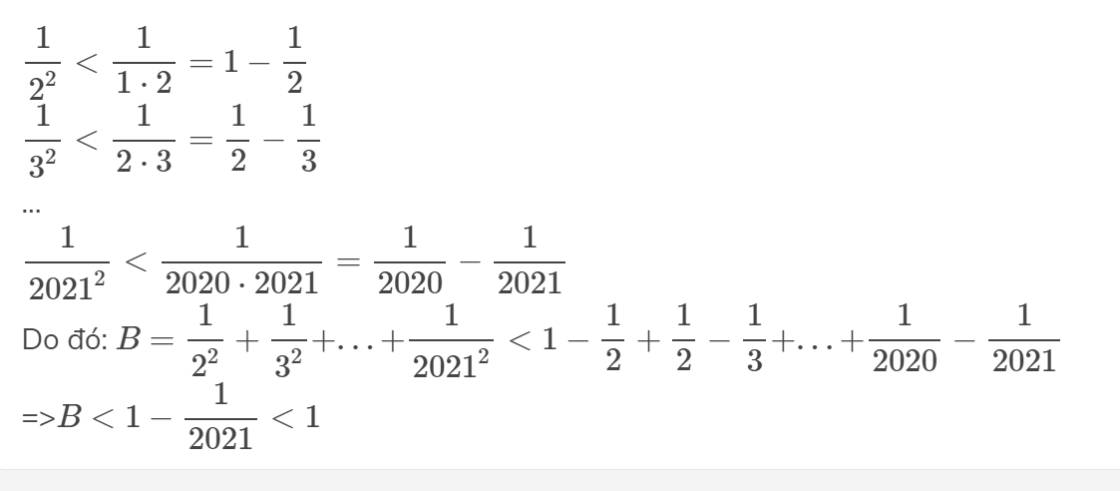
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{2021^2}< \dfrac{1}{2020\cdot2021}=\dfrac{1}{2020}-\dfrac{1}{2021}\)
Do đó: \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2021^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\)
=>\(B< 1-\dfrac{1}{2021}< 1\)

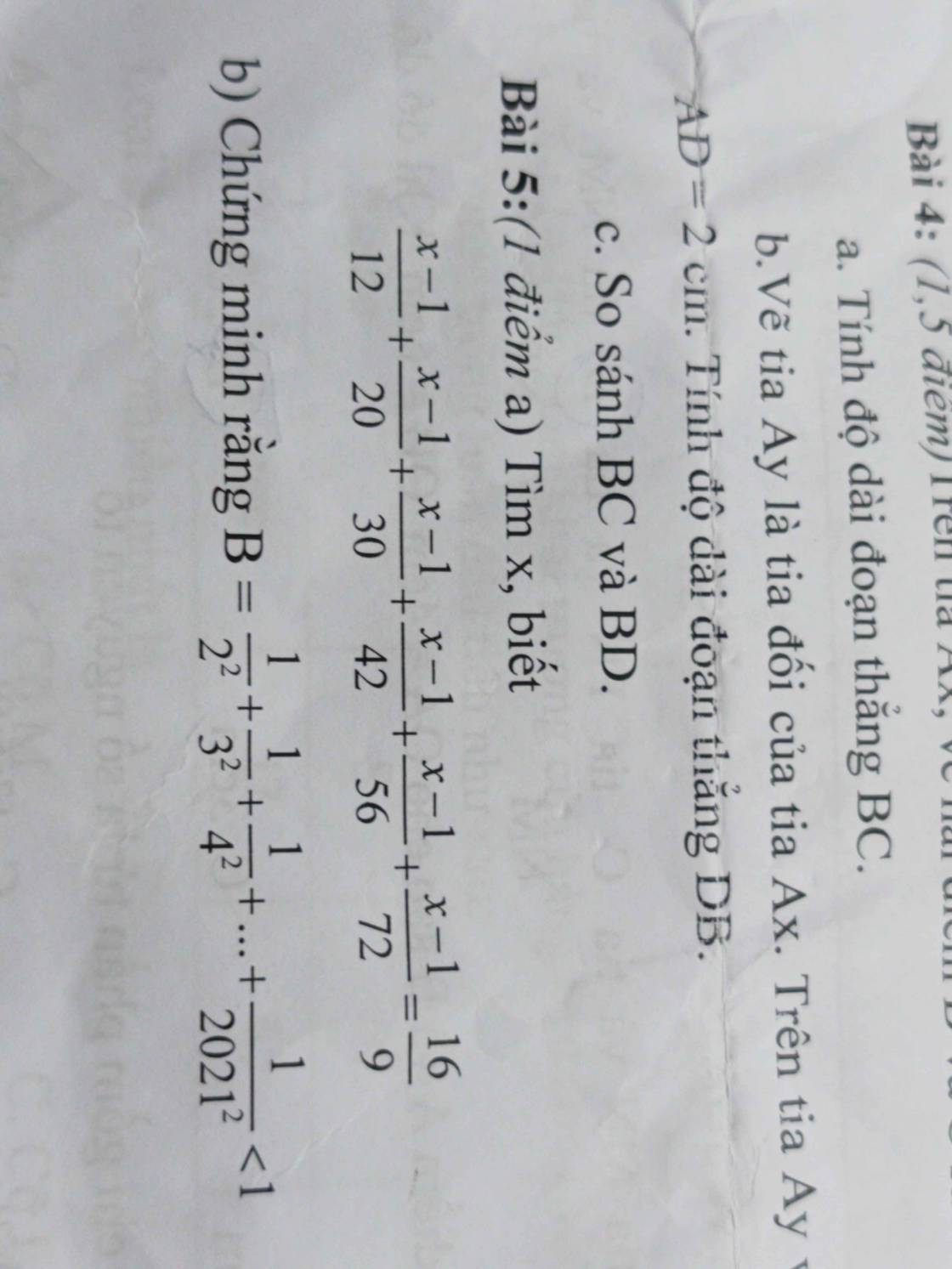
a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔNMI=ΔNKI
b: ta có: ΔNMI=ΔNKI
=>IM=IK
mà IK<IP(ΔIKP vuông tại K)
nên IM<IP
c: Xét ΔIMQ vuông tại M và ΔIKP vuông tại K có
IM=IK
\(\widehat{MIQ}=\widehat{KIP}\)(hai góc đối đỉnh)
Do đó: ΔIMQ=ΔIKP
=>IQ=IP
=>ΔIQP cân tại I
Xét ΔNQP có
QK,PM là các đường cao
QK cắt PM tại I
Do đó: I là trực tâm của ΔNQP
=>NI\(\perp\)PQ tại D
=>ND\(\perp\)PQ
MI < IP mà