As soon as i got home, I realized I'd left my bag in the shop
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


exercise 5: viết lại câu
1) No one in my class is more intelligent than Lan.
= Lan is the most intelligent in my class .
2) WE DON'T KNOW A HAPPIER PERSON THAN IM.
= HE IS HAPPIEST PERSON WE KNOW .

ĐKXĐ : x ≠ -2021
( bài này xét x > 0 nhé, x ≤ 0 thì tìm không ra đâu )
Áp dụng bất đẳng thức AM-GM ta có :
\(x+2021\ge2\sqrt{2021x}\)
=> \(\left(x+2021\right)^2\ge8084x\)
=> \(\frac{1}{\left(x+2021\right)^2}\le\frac{1}{8084x}\)
=> \(\frac{x}{\left(x+2021\right)^2}\le\frac{1}{8084}\)
Đẳng thức xảy ra <=> x = 2021
Vậy GTLN của biểu thức = 1/8084, đạt được khi x = 2021
** Bài này đúng với mọi số \(x\in\left\{x|x\inℝ,x\ne-2021\right\}\)chứ không riêng gì x > 0.
Ta có: \(\frac{x}{\left(x+2021\right)^2}=\left(\frac{x}{\left(x+2021\right)^2}-\frac{1}{8084}\right)+\frac{1}{8084}=\frac{-\left(x-2021\right)^2}{8084\left(x+2021\right)^2}+\frac{1}{8084}\le\frac{1}{8084}\)
Đẳng thức xảy ra khi x = 2021

Chị ơi câu 1 viết lại là Mai's sister is uglier than Mai . Câu 2 viết lại là Ha Noi is noisier than Hai Duong
Em gửi bài chị nhé
Chào em, em tham khảo nhé!
1) Mai is prettier than her sister
= Mai's sister isn't prettier than her.
2) Hai Duong isn't so noisy as Ha Noi.
= Ha Noi is noisier than Hai Duong.
Chúc em học tốt và có những trải nghiệm tuyệt vời tại olm.vn!

Bài 3 : Theo bài ra ta có : \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\Leftrightarrow x=3;2\)(*)
\(x+\left(x-2\right)\left(2x+1\right)=2\)
\(\Leftrightarrow x-2+\left(x-2\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x+2\right)=0\Leftrightarrow x=2;-1\)(**)
Dựa vào (*) ; (**) dễ dàng chứng minh được a;b nhé
c, Ko vì phương trình (*) ko có nghiệm -1 hay phương trình (**) ko có nghiệm 3 nên 2 phương trình ko tương đương

\(\left(x^2+x\right)\left(x^2+x+2\right)=-1\)
\(\Leftrightarrow\left(x^2+x+1-1\right)\left(x^2+x+1+1\right)=-1\)
\(\Leftrightarrow\left(x^2+x+1\right)^2-1^2=-1\)
\(\Leftrightarrow\left(x^2+x+1\right)^2=0\)
\(\Leftrightarrow x^2+x+1=0\)(vô nghiệm)

a) đkxđ: \(x\ne\pm2\)
Ta có: \(\frac{x+2}{x-2}-\frac{x-2}{x+2}=\frac{4}{x^2-4}\)
\(\Leftrightarrow\frac{\left(x+2\right)^2-\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow8x=4\)\(\Rightarrow x=\frac{1}{2}\)
b) đkxđ: \(x\ne\left\{1;-3\right\}\)
PT \(\Leftrightarrow\frac{\left(x+1\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)+4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Rightarrow x^2+4x+3-x^2-x+2+4=0\)
\(\Leftrightarrow3x+10=0\Rightarrow x=-\frac{10}{3}\)
c) đkxđ: \(x\ne\left\{0;-1\right\}\)
\(PT\Leftrightarrow\frac{\left(x-1\right)\left(x+1\right)+1-2x}{x\left(x+1\right)}=\frac{x}{x\left(x+1\right)}\)
\(\Rightarrow x^2-1+1-2x=x\)
\(\Leftrightarrow x^2-3x=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\left(ktm\right)\\x=3\left(tm\right)\end{cases}}\)
d) đkxđ: \(x\ne\left\{1;5\right\}\)
\(PT\Leftrightarrow\frac{x-1-3}{\left(x-1\right)\left(x-5\right)}=\frac{5\left(x-5\right)}{\left(x-1\right)\left(x-5\right)}\)
\(\Rightarrow x-4=5x-25\)
\(\Leftrightarrow4x=21\Rightarrow x=\frac{21}{4}\)
e) đkxđ: \(x\ne\left\{0;-2;2\right\}\)
\(PT\Leftrightarrow\frac{-2x+x+2}{x\left(x-2\right)\left(x+2\right)}=\frac{\left(x-4\right)\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow-x+2=x^2-6x+8\)
\(\Leftrightarrow x^2-5x+6=0\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\Rightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)

\(\frac{1}{x^2}+\frac{2}{x^2+1}+\frac{3}{x^2+2}+\frac{4}{x^2+3}=4\)
\(\Leftrightarrow\frac{1}{x^2}-1+\frac{2}{x^2+1}-1+\frac{3}{x^2+2}-1+\frac{4}{x^2+3}-1=0\)
\(\Leftrightarrow\frac{1-x^2}{x^2}+\frac{1-x^2}{x^2+1}+\frac{1-x^2}{x^2+2}+\frac{1-x^2}{x^2+3}=0\)
\(\Leftrightarrow1-x^2=0\Leftrightarrow x=\pm1\)

\(\frac{x+1}{x^2+x+1}-\frac{x-1}{x^2-x+1}=\frac{2\left(x+2\right)^2}{x^6-1}\)(ĐK: \(x\ne\pm1\))
\(\Leftrightarrow\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{2\left(x+2\right)^2}{\left(x^3-1\right)\left(x^3+1\right)}\)
\(\Leftrightarrow\frac{x^2-1}{x^3-1}-\frac{x^2-1}{x^3+1}=\frac{2\left(x+2\right)^2}{x^6-1}\)
\(\Leftrightarrow\left(x^2-1\right)\frac{x^3+1-\left(x^3-1\right)}{x^6-1}=\frac{2\left(x+2\right)^2}{x^6-1}\)
\(\Rightarrow x^2-1=\left(x+2\right)^2\)
\(\Leftrightarrow x=-\frac{5}{4}\)(thử lại thỏa mãn).

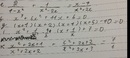
Khi về đến nhà, Tôi Nhận ra tôi đã để quên túi xách ở cửa hàng
Khi về đến nhà,tôi nhận ra mình đã quên túi ở cửa hàng