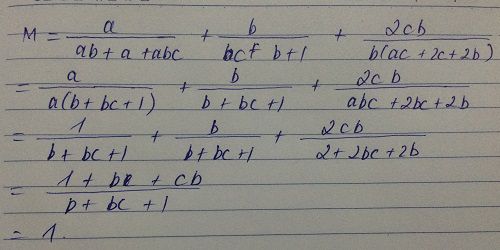Những người muôn năm cũ, Hồn ở đâu bây giờ. Em hiểu hồn trong câu trên nghĩa là gì?

những người muôn năm cũ. hồn ở đâu bây giờ

hồn ở đây được coi là những người thuê viết chữ trong ngày tết. Câu hỏi tu từ như xoáy vào tâm can của người đọc về những nét đẹp tinh hoa của dân tộc dã vĩnh viễn chìm vào quá khứ. Khổ cuối thể hiện khung cảnh quen thuộc trong ngày Tết cổ truyền năm xưa đã thuộc về dĩ vãng, xưa cũ, quá khứ. Cho đến khi phong tục phương Tây xâm nhập vào nước ta thời ấy, ông đồ không còn được đắc ý như xưa cũ nữa, và những người thuê viết đã đi mất. Ông đồ vẫn ngồi đấy. 

Hồn ở trong câu trên thể hiện tính bộc lộ tình cảm, cảm xúc của tác giả.

Kẻ \(CH//AG\)và các điểm như hình vẽ. 

Trong tam giác \(BCF\): \(\widehat{FBC}+\widehat{BCF}+\widehat{CFB}=180^o\). 

Trong tam giác \(ADE\): \(\widehat{DAE}+\widehat{DEA}+\widehat{ADE}=180^o\)

\(BC//AD\Rightarrow\widehat{FBC}=\widehat{EDA}\)(Hai góc so le trong) 

\(CH//AG\Rightarrow\widehat{CFB}=\widehat{AED}\)(Hai góc so le trong) 

Suy ra \(\widehat{BCF}=\widehat{DAE}\).

Xét tam giác \(DAE\)và tam giác \(BCF\)có: 

\(\widehat{BCF}=\widehat{DAE}\)(cmt)

\(DA=BC\)(tính chất hình bình hành)

\(\widehat{CBF}=\widehat{ADE}\)(cmt)

Suy ra \(\Delta DAE=\Delta BCF\). 

Suy ra \(DE=BF\)(hai cạnh tương ứng). 

Có: \(\frac{DG}{GC}=\frac{DE}{EF}=\frac{DE}{EB-BF}=\frac{DE}{EB-DE}\Rightarrow\frac{GC}{DG}=\frac{EB-DE}{DE}=4-1=3\Rightarrow\frac{DG}{GC}=\frac{1}{3}\)

Ta có: \(M=\frac{1}{\left(x-2\right).\left(x-3\right)}+\frac{1}{\left(x-3\right).\left(x-4\right)}+\frac{1}{\left(x-4\right).\left(x-5\right)}+\frac{1}{\left(x-5\right).\left(x-6\right)}\)

   \(\Leftrightarrow M=\frac{1}{x-2}-\frac{1}{x-3}+\frac{1}{x-3}-\frac{1}{x-4}+\frac{1}{x-4}-\frac{1}{x-5}+\frac{1}{x-5}-\frac{1}{x-6}\)

   \(\Leftrightarrow M=\frac{1}{x-2}-\frac{1}{x-6}\)

   \(\Leftrightarrow M=\frac{x-6-x+2}{\left(x-2\right).\left(x-6\right)}\)

   \(\Leftrightarrow M=-\frac{4}{x^2-8x+12}\)

tau đéo biết

Vì \(abc=2\)nên ta có:

\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)

\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)

\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)

\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)

\(=\frac{1+b+bc}{bc+c+1}=1\)

câu trả lời;

ĐKXĐ : x ≠ ±1

pt <=> \(\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}-\frac{4}{\left(x-1\right)\left(x+1\right)}=0\)

<=> \(\frac{x^2+2x+1-x^2+2x-1-4}{\left(x-1\right)\left(x+1\right)}=0\)

<=> \(\frac{4x-4}{\left(x-1\right)\left(x+1\right)}=0\)

=> 4x - 4 = 0 

<=> x = 1 ( ktm )

Vậy phương trình vô nghiệm 

Gọi h(x) là thương trong phép chia f(x) cho g(x)

Vì f(x) bậc 3, g(x) bậc 2 => h(x) bậc nhất

=> h(x) có dạng cx + d

f(x) ⋮ g(x) <=> f(x) = g(x).h(x)

<=> x³ + ax² + 2x + b = ( x² + x + 1 )( cx + d )

<=> x³ + ax² + 2x + b = cx³ + dx² + cx² + dx + cx + d

<=> x³ + ax² + 2x + b = cx³ + ( d + c )x² + ( d + c )x + d

Đồng nhất hệ số ta có :

\(\hept{\begin{cases}c=1\\d+c=a=2\\d=b\end{cases}}\Rightarrow\hept{\begin{cases}a=2\\b=c=d=1\end{cases}}\)

Vậy a = 2 , b = 1

Vì \(f \left(x\right)⋮g\left(x\right)\)\(\Rightarrow\)\(f\left(x\right)=g\left(x\right).Q\left(x\right)\)     

Đặt \(Q\left(x\right)=cx+d\)          \(\left(c,d\ne0\right)\)

\(\Rightarrow\)\(f\left(x\right)=\left(x^2+x+1\right).\left(cx+d\right)\)

\(\Leftrightarrow\)\(f\left(x\right)=cx^3+dx^2+cx^2+dx+cx+d\)

\(\Leftrightarrow\)\(x^3+ax^2+2x+b=cx^3+\left(d+c\right)x+\left(d+c\right)x+d\)

Đồng nhất hệ số, ta có:

      \(c=1\)                                             \(a=2\)

      \(d+c=a\)              \(\Leftrightarrow\)           \(b=1\)

      \(d+c=2\)                                    \(c=1\)\(\left(TM\right)\)

      \(d=b\)                                             \(d=1\)\(\left(TM\right)\)

Vậy \(f \left(x\right)⋮g\left(x\right)\)khi  \(\hept{\begin{cases}a=2\\b=1\end{cases}}\)