Bài trình chiếu thường được sử dụng để trình bày thông tin một cách rõ ràng và hấp dẫn.

trình bày những nội dung mà người trình bày muốn cho mọi người xem

Giá tiền của 1 quyển vở là:

120000:15=8000(đồng)

Số tiền Minh phải trả là \(120000\times\dfrac{2}{3}=80000\left(đồng\right)\)

Số quyển vở Minh mua là:

80000:8000=10(quyển)

35

1100

Bài 1:

a: Ta có: Ot là phân giác của góc xOy

=>\(\widehat{xOt}=\widehat{yOt}=\dfrac{180^0}{2}=90^0\)

=>BO\(\perp\)DC

Xét ΔOAC vuông tại A và ΔODB vuông tại D có

OA=OD

OC=OB

Do đó: ΔOAC=ΔODB

=>AC=DB(1)

Ta có: ΔOAC=ΔODB

=>\(\widehat{OAC}=\widehat{ODB}\)

mà \(\widehat{OAC}+\widehat{OCA}=90^0\)

nên \(\widehat{ODB}+\widehat{OCA}=90^0\)

=>CA\(\perp\)BD

b: Ta có;ΔOAC vuông tại O

mà OM là đường trung tuyến

nên \(OM=\dfrac{AC}{2}\)(3)

=>OM=MA=MC

Ta có: ΔOBD vuông tại O

mà ON là đường trung tuyến

nên \(ON=\dfrac{BD}{2}\)(2)

=>ON=NB=ND

Từ (1),(2),(3) suy ra OM=ON

c: NB=NO nên \(\widehat{NBO}=\widehat{NOB}\)

MA=MO

nên \(\widehat{MAO}=\widehat{MOA}\)

\(\widehat{NOM}=\widehat{NOA}+\widehat{MOA}\)

\(=\widehat{NBO}+\widehat{MAO}=\widehat{DBO}+\widehat{CAO}\)

\(=\widehat{DBO}+\widehat{ODB}=90^0\)

=>ΔNOM vuông cân tại O

=>\(\widehat{ONM}=\widehat{OMN}=45^0\)

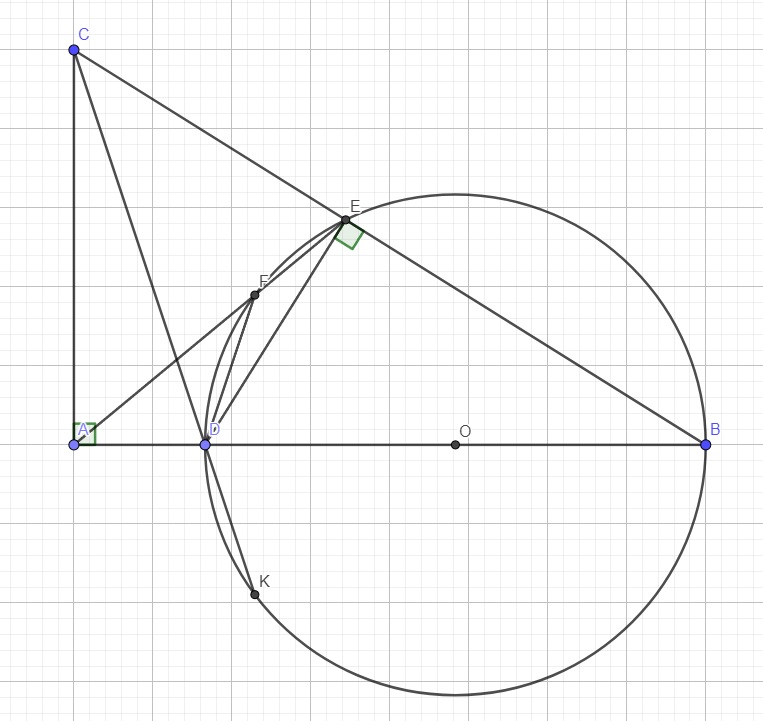
d: Xét ΔBDC có

CA,BO là các đường cao

CA cắt BO tại A

Do đó: A là trực tâm của ΔBDC
=>DA\(\perp\)BC

Tứ giác DBEF nội tiếp (O) nên \(\widehat{DBE}+\widehat{DFE}=180^0\)

Mà \(\widehat{DFE}+\widehat{DFA}=180^0\) (kề bù)

\(\Rightarrow\widehat{DFA}=\widehat{DBE}\)

Xét 2 tam giác ADF và AEB có:

\(\left\{{}\begin{matrix}\widehat{DAF}-chung\\\widehat{DFA}=\widehat{DBE}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta ADF\sim\Delta AEB\left(g.g\right)\)

\(\Rightarrow\dfrac{AF}{AB}=\dfrac{AD}{AE}\Rightarrow AE.AF=AD.AB\) (1)

Do BD là đường kính của (O) \(\Rightarrow\widehat{BED}=90^0\) (góc nt chắn nửa đường tròn)

Xét 2 tam giác BED và BAC có:

\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{BED}=\widehat{BAC}=90^0\end{matrix}\right.\)

\(\Rightarrow\Delta BED\sim\Delta BAC\left(g.g\right)\)

\(\Rightarrow\dfrac{BE}{AB}=\dfrac{BD}{BC}\Rightarrow BE.BC=AB.BD\) (2)

Từ (1); (2):

\(\Rightarrow AE.AF+BE.BC=AD.AB+AB.BD=AB\left(AD+BD\right)=AB^2\) (không đổi)

Here's an introduction to the Battle of Dien Bien Phu in English:

---

The Battle of Dien Bien Phu was a pivotal conflict in the First Indochina War, marking the climax of a struggle between French colonial forces and the Viet Minh, led by Uncle Ho Chi Minh. This battle took place between March and May 1954 in the Dien Bien Phu valley in northwestern Vietnam.

The French, under the command of General Christian de Castries, fortified the Dien Bien Phu valley, creating a complex series of strongpoints to defend against the expected Viet Minh assault. 

However, the Viet Minh, commanded by General Vo Nguyen Giap, executed an impressive logistical feat. They transported heavy artillery and supplies over mountainous terrain, manually hauling pieces through rugged paths. Once in position, they launched a massive and well-coordinated attack on the French positions, encircling and bombarding them with artillery, which the French had believed impossible.

The siege lasted for fifty-five days, with intense fighting characterized by trench warfare and direct assaults reminiscent of World War I battles. The Viet Minh's tactics and endurance in the face of French firepower eventually led to the fall of the French garrison.

The capture of Dien Bien Phu was a significant victory for the Viet Minh and a symbol of the rise of nationalist movements in colonial territories. It precipitated the Geneva Conference, which negotiated the ceasefire and eventually led to the withdrawal of French forces from Indochina. This battle not only marked the end of French colonial rule in Vietnam but also reshaped the geopolitical landscape of Southeast Asia.

Dien Bien Phu remains a testament to the strategic brilliance of General Giap and the resilience of the Vietnamese people. It stands as a historic reminder of the challenges of colonial warfare and the potent force of nationalist fervor.

Bài 1

Tổng số gạo hai xe chở được:

18/5 × 2 = 36/5 = 7,2 (tấn) = 72 (tạ)

2 tấn 2 tạ = 22 tạ

Số lượng gạo xe thứ nhất chở về kho:

(72 - 22) : 2 = 25 (tạ)

Bài 2

Tổng số hình dán của Mai và Mi:

60 + 40 = 100 (hình)

Số hình dán Mai cho Mi:

60 - 100 : 2 = 10 (hình)

Số hình dán Mai cho Mi so với số hình dán ban đầu của Mai:

10/60 : 1/6

Buổi sáng bán được: \(48\times\dfrac{2}{3}=32\left(m\right)\)

Buổi chiều bán được: \(48\times\dfrac{1}{6}=8\left(m\right)\)

Tấm vải còn lại:

48-32-8=8(m)

\(\left(4x-5\right)\left(\dfrac{5}{4}x-2\right)=1\dfrac{1}{3}\)

=>\(5x^2-8x-\dfrac{25}{4}x+10-\dfrac{4}{3}=0\)

=>\(5x^2-\dfrac{57}{4}x+\dfrac{26}{3}=0\)

\(\text{Δ}=\left(-\dfrac{57}{4}\right)^2-4\cdot5\cdot\dfrac{26}{3}=\dfrac{1427}{48}>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{\dfrac{57}{4}-\sqrt{\dfrac{1427}{48}}}{10}=\dfrac{57\sqrt{3}-\sqrt{1427}}{40\sqrt{3}}=\dfrac{171-\sqrt{4281}}{120}\\x_2=\dfrac{\dfrac{57}{4}+\sqrt{\dfrac{1427}{48}}}{10}=\dfrac{171+\sqrt{4281}}{120}\end{matrix}\right.\)

Lớp 6 mà anh.