Cho tam giác ABC cân tại A. D là trung điểm của cạnh BC. Lấy điểm E bất kì thuộc cạnh BC. M,N lần lượt là chân đường vuông góc kẻ từ E đến các cạnh AB, AC. Chứng minh DM=DN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Xét tam giác $ABI$ và $ACI$ có:
$AI$ chung
$AB=AC$ (do $ABC$ cân tại $A$)
$IB=IC$
$\Rightarrow \triangle ABI=\triangle ACI$ (c.c.c)
b.
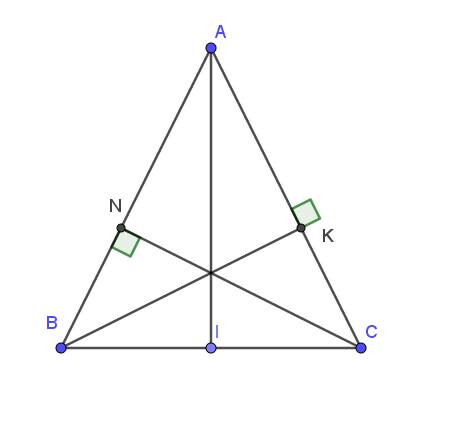
Xét tam giác $ABK$ và $ACN$ có:
$\widehat{A}$ chung
$\widehat{AKB}=\widehat{ANC}=90^0$
$AB=AC$
$\Rightarrow \triangle ABK=\triangle ACN$ (cạnh huyền - góc nhọn)
$\Rightarrow AK=AN$
$M$ là điểm nào bạn nhỉ?


Câu 4:
Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
Câu 5:
a: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI\(\perp\)BC tại I
Ta có: I là trung điểm của BC
=>\(IB=IC=\dfrac{BC}{2}=4\left(cm\right)\)
ΔAIB vuông tại I
=>\(AI^2+IB^2=AB^2\)
=>\(AI^2=5^2-4^2=9\)
=>AI=3(cm)
Xét ΔABC có
AI là đường trung tuyến
G là trọng tâm
Do đó: \(IG=\dfrac{1}{3}IA=\dfrac{1}{3}\cdot3=1\left(cm\right)\)
ΔBIG vuông tại I
=>\(IB^2+IG^2=GB^2\)
=>\(GB^2=4^2+1^2=17\)
=>\(GB=\sqrt{17}\left(cm\right)\)

a: \(Q\left(x\right)=2x^2+x^3-2x^2+3x+1-5x^4\)
\(=-5x^4+x^3+\left(2x^2-2x^2\right)+3x+1\)
\(=-5x^4+x^3+3x+1\)
b: Bậc là 4
Hệ số tự do là 1
Hệ số cao nhất là -5

Xét ΔMEN và ΔMEP có
ME chung
EN=EP
MN=MP
Do đó: ΔMEN=ΔMEP

\(Q\left(1\right)=a^3+2\cdot1^4-5\cdot1^2-2\cdot1^3-6\cdot1+3\\ =a^3+2\cdot1-5\cdot1-2\cdot1-6\cdot1+3\\ =a^3+2-5-2-6+3\\ =a^3-8\)
\(Q\left(1\right)=a^3+2\cdot1^4-5\cdot1^2-2\cdot1^3-6\cdot1+3\)
\(=a^3+2-5-2-6+3\)
\(=a^3-8\)

Ta có :
\(x^3-3x^2+2x-6\\ =\left(x^3-3x^2\right)+\left(2x-6\right)\\ =x^2\left(x-3\right)+2\left(x-3\right)\\ =\left(x-3\right)\left(x^2+2\right)\)
Vậy `(x-3)(x^2 +2) : (x-3)=x^2+2`
\(\dfrac{x^3-3x^2+2x-6}{x-3}\)
\(=\dfrac{x^2\left(x-3\right)+2\left(x-3\right)}{x-3}\)
\(=x^2+2\)

Gọi O là trung điểm của AE
Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC và AD\(\perp\)BC
=>\(\widehat{BAD}=\widehat{CAD}\left(3\right)\)
Vì \(\widehat{AME}=\widehat{ADE}=\widehat{ANE}=90^0\)
nên A,M,E,D,N cùng thuộc đường tròn đường kính AE
=>A,M,E,D,N cùng thuộc (O)
Xét (O) có
\(\widehat{DMN}\) là góc nội tiếp chắn cung DN
\(\widehat{DAN}\) là góc nội tiếp chắn cung DN
Do đó: \(\widehat{DMN}=\widehat{DAN}\)(1)
Xét (O) có
\(\widehat{DNM}\) là góc nội tiếp chắn cung DM
\(\widehat{DAM}\) là góc nội tiếp chắn cung DM
Do đó: \(\widehat{DNM}=\widehat{DAM}\left(2\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DMN}=\widehat{DNM}\)
=>DM=DN
Đề sai. Bạn xem lại đề.