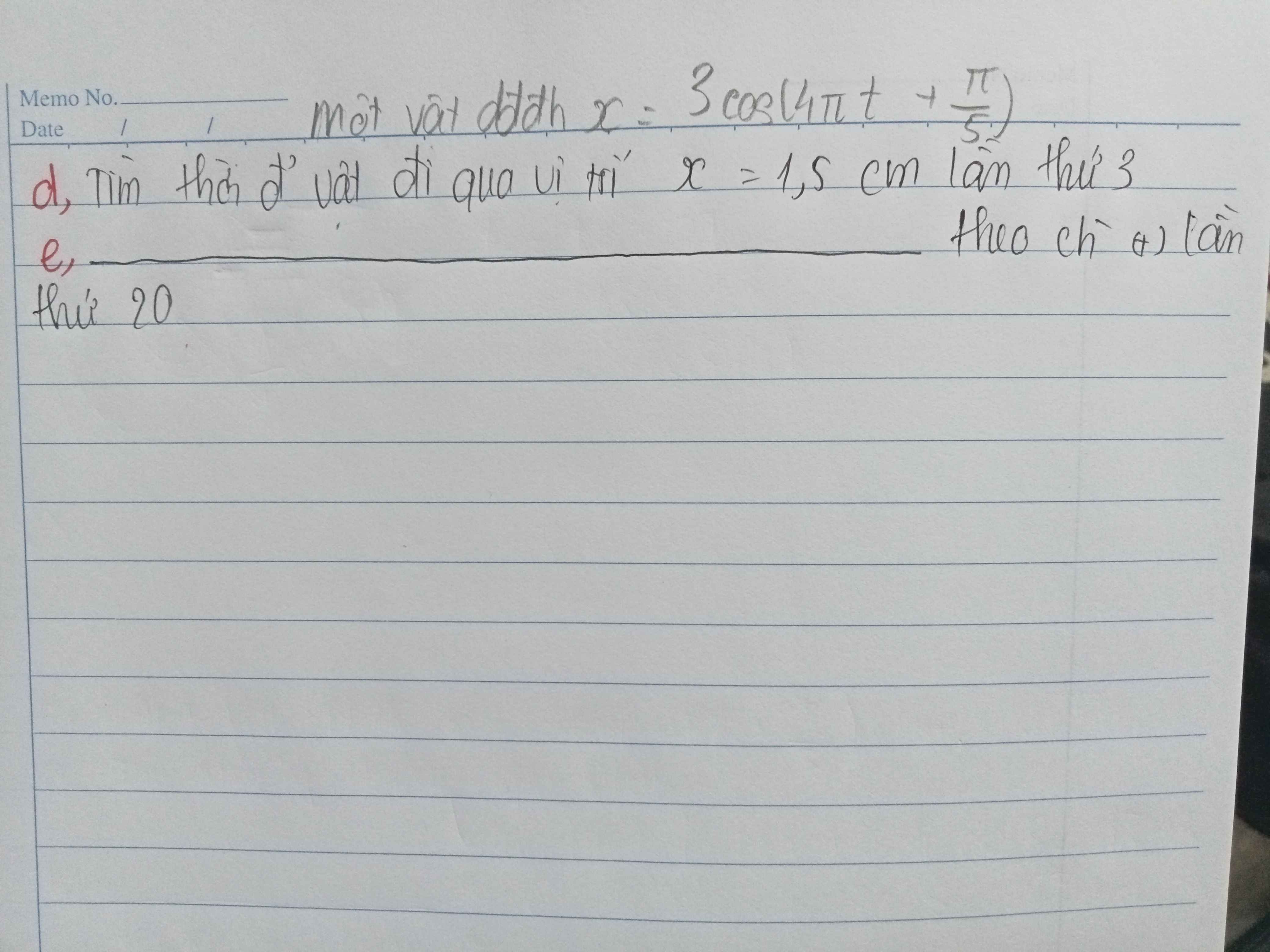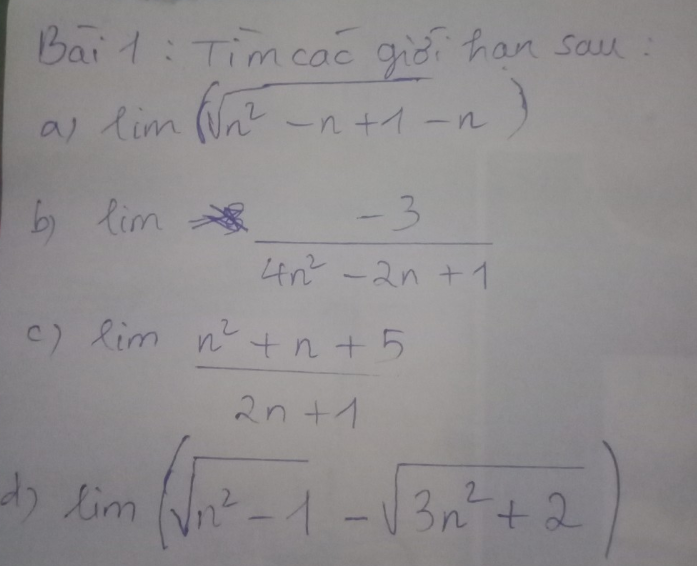d) \(A=3cm\); \(\omega=4\pi\left(rad/s\right)\); \(\varphi_0=\dfrac{\pi}{5}\left(rad\right)\)

Khi đó \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)

Cho \(x=1,5cm\Leftrightarrow\varphi=\pm\dfrac{\pi}{3}\left(rad\right)\) 

Thời gian vật đi qua vị trí \(x=1,5cm\) lần thứ ba là:

\(T+t_d=0,5+\dfrac{\Delta\varphi_d}{2\pi}.T\)

\(=0,5+\dfrac{\dfrac{\pi}{3}-\dfrac{\pi}{5}}{2\pi}.0,5\)

\(=\dfrac{8}{15}\left(s\right)\)

e) Thời gian cần tìm là:

\(t_e+19T=\dfrac{\Delta\varphi_e}{2\pi}.T+19.0,5\) 

\(=\dfrac{\dfrac{4\pi}{3}}{2\pi}.0,5+9.5=\dfrac{59}{6}\left(s\right)\) 

a) \(\lim\limits_{ }\left(\sqrt{n^2-n+1}-n\right)\)

\(=\lim\limits_{ }\left[\dfrac{\left(\sqrt{n^2-n+1}-n\right)\left(\sqrt{n^2-n+1}+n\right)}{\sqrt{n^2-n+1}+n}\right]\)

\(=\lim\limits_{ }\left(\dfrac{1-n}{\sqrt{n^2-n+1}+n}\right)\)

\(=\lim\limits_{ }\left(\dfrac{\dfrac{1}{n}-1}{\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}+1}\right)\)

\(=-\dfrac{1}{2}\)

b) \(\lim\limits_{ }\left(\dfrac{-3}{4n^2-2n+1}\right)=0\)

c) \(\lim\limits_{ }\dfrac{n^2+n+5}{2n+1}=+\infty\)

d) \(\lim\limits_{ }\left(\sqrt{n^2-1}-\sqrt{3n^2+2}\right)\)

\(=\lim\limits_{ }\left(\dfrac{-2n^2-3}{\sqrt{n^2-1}+\sqrt{3n^2+2}}\right)\)

\(\lim\limits_{ }\left(\dfrac{-2n-\dfrac{3}{n}}{\sqrt{1-\dfrac{1}{n^2}}+\sqrt{3+\dfrac{2}{n^2}}}\right)\)

\(=-\infty\)

a: \(lim\left(\sqrt{n^2-n+1}-n\right)\)

\(=\lim\limits\dfrac{n^2-n+1-n^2}{\sqrt{n^2-n+1}+n}=\lim\limits\dfrac{-n+1}{\sqrt{n^2-n+1}+n}\)

\(=\lim\limits\dfrac{-1+\dfrac{1}{n}}{\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}+1}=\dfrac{-1+0}{\sqrt{1-0+0}+1}=\dfrac{-1}{2}\)

b: \(\lim\limits\dfrac{-3}{4n^2-2n+1}\)

\(=\lim\limits\dfrac{-\dfrac{3}{n^2}}{4-\dfrac{2}{n}+\dfrac{1}{n^2}}=\dfrac{0}{4-0+0}=0\)

c: \(\lim\limits\dfrac{n^2+n+5}{2n+1}=\lim\limits\dfrac{n^2\left(1+\dfrac{1}{n}+\dfrac{5}{n^2}\right)}{n\left(2+\dfrac{1}{n}\right)}\)

\(=\lim\limits\dfrac{n\left(1+\dfrac{1}{n}+\dfrac{5}{n^2}\right)}{2+\dfrac{1}{n}}=+\infty\)

d: \(\lim\limits\left(\sqrt{n^2-1}-\sqrt{3n^2+2}\right)\)

\(=\lim\limits\left(\dfrac{n^2-1-3n^2-2}{\sqrt{n^2-1}+\sqrt{3n^2+2}}\right)=\lim\limits\left(\dfrac{-2n^2-3}{\sqrt{n^2-1}+\sqrt{3n^2+2}}\right)\)

\(=\lim\limits\left(\dfrac{n^2\left(-2-\dfrac{3}{n^2}\right)}{n\cdot\left(\sqrt{1-\dfrac{1}{n^2}}+\sqrt{3+\dfrac{2}{n^2}}\right)}\right)\)

\(=\lim\limits\left(\dfrac{n\left(-2-\dfrac{3}{n^2}\right)}{\sqrt{1-\dfrac{1}{n^2}}+\sqrt{3+\dfrac{2}{n^2}}}\right)=+\infty\)

a:

d:

\(\dfrac{sin^3x+sinx\cdot cos^2x-cosx}{1-2\cdot sinx\cdot cosx}\)

\(=\dfrac{sinx\left(sin^2x+cos^2x\right)-cosx}{\left(sinx-cosx\right)^2}\)

\(=\dfrac{sinx-cosx}{\left(sinx-cosx\right)^2}=\dfrac{1}{sinx-cosx}\)