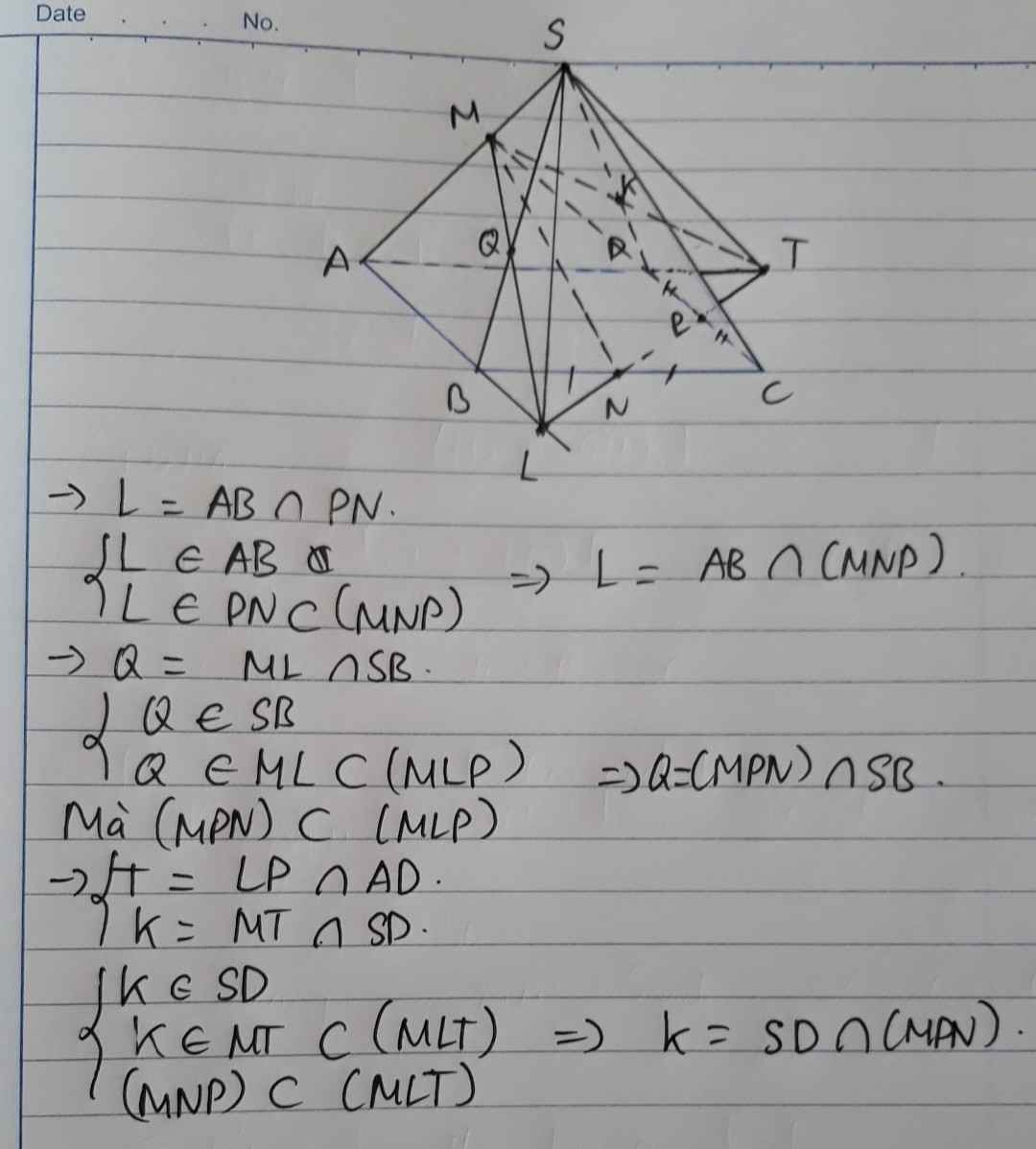
b: Chọn mp(SAC) có chứa SC

\(I\in SA\subset\left(SAC\right);I\in\left(BIK\right)\)

Do đó: \(I\in\left(SAC\right)\cap\left(BIK\right)\)

Trong mp(ABCD), gọi H là giao điểm của AC và BK

=>\(H\in\left(SAC\right)\cap\left(BIK\right)\)

=>\(\left(SAC\right)\cap\left(BIK\right)=HI\)

Gọi M là giao điểm của HI với SC

=>M là giao điểm của SC với mp(BIK)

\(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\Rightarrow1+2^2=\dfrac{1}{cos^2\alpha}\\ \Rightarrow5=\dfrac{1}{cos^2\alpha}\Rightarrow cos^2\alpha=\dfrac{1}{5}\)

tôi quá mong manh

yeah

tìm chữ số tận cùng :7^1+7^2+...+7^50.giúp mình với ạ .Cảm ơn mọi người

bạn gửi câu hỏi nhầm chỗ rồi nhé!

\(0< a< \dfrac{\Omega}{2}\)

=>\(sina>0\)

=>\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\)

\(\dfrac{3}{2}\Omega< b< 2\Omega\)

=>\(sinb< 0\)

=>\(sinb=-\sqrt{1-\left(\dfrac{12}{13}\right)^2}=-\dfrac{5}{13}\)

\(tana=\dfrac{sina}{cosa}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)

\(tanb=\dfrac{sinb}{cosb}=\dfrac{-5}{13}:\dfrac{12}{13}=-\dfrac{5}{12}\)

\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana\cdot tanb}\)

\(=\dfrac{\dfrac{4}{3}+\dfrac{-5}{12}}{1-\dfrac{4}{3}\cdot\dfrac{-5}{12}}=\dfrac{11}{12}:\left(1+\dfrac{20}{36}\right)=\dfrac{11}{12}:\dfrac{14}{9}\)

\(=\dfrac{11}{12}\cdot\dfrac{9}{14}=\dfrac{11\cdot3}{4\cdot14}=\dfrac{33}{56}\)

Giúp em vs ạ