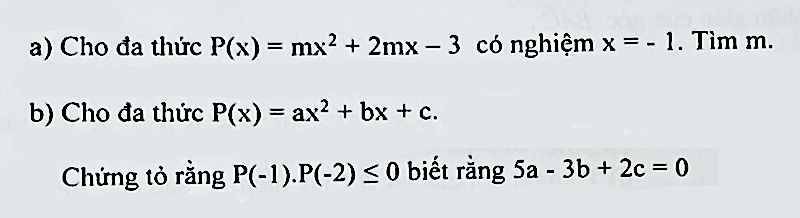
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong hình học Euclid, một tam giác thường được xác định bởi ba cạnh và ba góc. Để một tam giác tồn tại, ta cần biết điều kiện cho ba cạnh và ba góc. Trong trường hợp bạn đề cập, nếu ta có một cạnh là góc vuông và một góc nhọn không kề cạnh với góc vuông đó, thì sẽ xảy ra mâu thuẫn.
Vì trong một tam giác, tổng các góc bằng 180 độ, và trong một tam giác vuông, một góc là 90 độ. Nếu một góc khác không kề với góc vuông, nó sẽ phải nằm ở phần còn lại của tam giác, tức là từ 180 độ trừ đi 90 độ, tức là 90 độ. Nhưng điều này không thể xảy ra vì trong tam giác, không thể có góc nào lớn hơn 90 độ.
Vậy nên, một tam giác với một cạnh là góc vuông và một góc nhọn không kề cạnh với nó không thể tồn tại trong hình học Euclid.

a) ∆ABC vuông tại A (gt)
⇒ ∠ABC + ∠BCA = 90⁰ (hai góc nhọn trong tam giác vuông phụ nhau)
b) Do CE là đường phân giác của ∆ABC (gt)
⇒ CE là tia phân giác của ∠ACB
⇒ ∠ACE = ∠BCE
⇒ ∠ACE = ∠HCE
Xét hai tam giác vuông: ∆ACE và ∆HCE có:
CE là cạnh chung
∠ACE = ∠HCE (cmt)
⇒ ∆ACE = ∆HCE (cạnh huyền - góc nhọn)
⇒ AC = HC (hai cạnh tương ứng)
c) Do ∆ACE = ∆HCE (cmt)
⇒ AE = HE (hai cạnh tương ứng)
⇒ E nằm trên đường trung trực của AH (1)
Do AC = HC (cmt)
⇒ C nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ CE là đường trung trực của AH
Mà I là giao điểm của AH và CE (gt)
⇒ I là trung điểm của AH
⇒ IA = IH
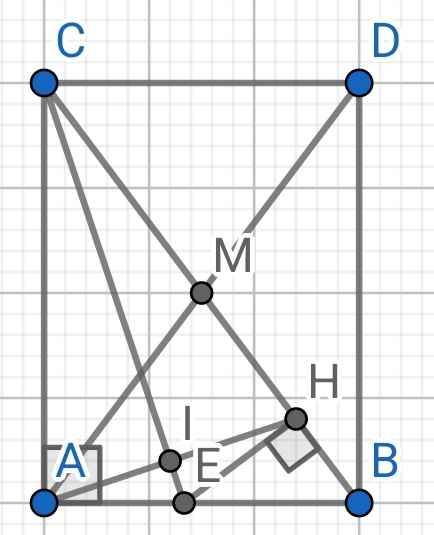
d) Trên tia đối của tia MA lấy điểm D sao cho AM = DM
⇒ M là trung điểm của AD
Do M là trung điểm của BC (gt)
⇒ BM = CM
Xét ∆ABM và ∆DCM có:
AM = DM
∠AMB = ∠DMC (đối đỉnh)
BM = CM (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
⇒ ∠BAM = ∠CDM (hai góc tương ứng)
Mà ∠BAM và ∠CDM là hai góc so le trong
⇒ AB // CD
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ CD ⊥ AC
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABD và ∆CDB có:
AB = CD (cmt)
DB là cạnh chung
⇒ ∆ABD = ∆CDB (hai cạnh góc vuông)
⇒ AD = BC (hai cạnh tương ứng)
Mà M là trung điểm của AD (cmt)
⇒ AD = 2AM
⇒ BC = 2AM

Lời giải:
a. Xét tam giác $ABM$ và $HBM$ có:
$\widehat{BAM}=\widehat{BHM}=90^0$
$\widehat{ABM}=\widehat{HBM}$ (do $BM$ là phân giác $\widehat{B}$)
$BM$ chung
$\Rightarrow \triangle ABM=\triangle HBM$ (ch-gn)
b.
Tam giác $MCH$ vuông tại $H$ nên cạnh huyền $MC$ là cạnh lớn nhất trong tam giác
$\Rightarrow MC> CH$
c.
Từ tam giác bằng nhau phần a suy ra $AM=MH$
Xét tam giác $AMK$ và $HMC$ có:
$\widehat{MAK}=\widehat{MHC}=90^0$
$AM=MH$
$\widehat{AMK}=\widehat{HMC}$ (đối đỉnh)
$\Rightarrow \triangle AMK=\triangle HMC$ (g.c.g)
$\Rightarrow MK=MC$
$\Rightarrow MKC$ cân tại $M$.

** Bổ sung điều kiện $a,b,c,d>0$
Lời giải:
Đặt biểu thức đã cho là $A$.
Với $a,b,c,d>0$ thì:
$A>\frac{a}{a+b+c+d}+\frac{b}{a+b+c+d}+\frac{c}{a+b+c+d}+\frac{d}{a+b+c+d}=1(*)$
Mặt khác:
Xét hiệu:
$\frac{a}{a+b+c}-\frac{a+d}{a+b+c+d}=\frac{-(bd+dc)}{(a+b+c)(a+b+c+d)}<0$ với $a,b,c,d>0$
$\Rightarrow \frac{a}{a+b+c}< \frac{a+d}{a+b+c+d}$
Hoàn toàn tương tự ta cũng có:
$\frac{b}{a+b+d}< \frac{b+c}{a+b+c+d}$
$\frac{c}{b+c+d}< \frac{c+a}{a+b+c+d}$
$\frac{d}{a+c+d}< \frac{d+b}{a+b+c+d}$
Cộng theo vế các BĐT trên thì:
$A< \frac{a+d+b+c+c+a+d+b}{a+b+c+d}=\frac{2(a+b+c+d)}{a+b+c+d}=2(**)$
Từ $(*); (**)\Rightarrow 1< A< 2$
$\Rightarrow A$ không là số tự nhiên.
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.


Gọi số quyển sách của An,Bình, Cường lần lượt là a(quyển),b(quyển),c(quyển)
(ĐK: \(a,b,c\in Z^+\))
Số sách của An,Bình,Cường lần lượt tỉ lệ với 3;4;5 nên \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Số sách của Bình ít hơn tổng quyển sách của An và Cường là 8 quyển nên a+c-b=8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+c-b}{3+5-4}=\dfrac{8}{4}=2\)
=>a=3*2=6; b=2*4=8; c=2*5=10
vậy: số quyển sách của An,Bình, Cường lần lượt là 6 quyển; 8 quyển; 10 quyển

Giải
a; Gọi giá tiền của cây thước là y (đồng)
Số tiền còn lại của Lan sau khi mua là
200 000 - y - 2y = 200 000 - 3y (đồng)
b; Số tiền còn lại của Lan sau khi mua một cây thước là:
200 000 - y
Số bút mà Lan có thể mua là:
\(\dfrac{200000-y}{2y}\)


Lời giải:
a. Vì $P(x)$ có nghiệm $x=-1$ nên:
$P(-1)=0$
$\Leftrightarrow m(-1)^2+2m(-1)-3=0$
$\Leftrightarrow m-2m-3=0$
$\Leftrightarrow -m-3=0\Leftrightarrow m=-3$
b.
Có:
$P(-1)=a(-1)^2+b(-1)+c=a-b+c$
$P(-2)=a(-2)^2+b(-2)+c=4a-2b+c$
$\Rightarrow P(-1)+P(-2)=5a-3b+2c=0$
$\Rightarrow P(-1)=-P(-2)$
$\Rightarrow P(-1)P(-2)=-P(-2)P(-2)=-P^2(-2)\leq 0$ (đpcm)