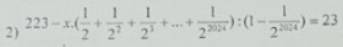
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2x=3y
=>\(\dfrac{x}{3}=\dfrac{y}{2}\)
=>\(\dfrac{x}{21}=\dfrac{y}{14}\left(1\right)\)
5y=7z
=>\(\dfrac{y}{7}=\dfrac{z}{5}\)
=>\(\dfrac{y}{14}=\dfrac{z}{10}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)
Đặt \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=k\)
=>x=21k; y=14k; z=10k
3x-2y+5z=-30
=>\(3\cdot21k-2\cdot14k+5\cdot10k=-30\)
=>85k=-30
=>\(k=-\dfrac{30}{85}=-\dfrac{6}{17}\)
=>\(x=21\cdot\dfrac{-6}{17}=\dfrac{-126}{17};y=14\cdot\dfrac{-6}{17}=-\dfrac{84}{17};z=10\cdot\dfrac{-6}{17}=-\dfrac{60}{17}\)
\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\)
\(5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\)
\(\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=\dfrac{3x}{63}=\dfrac{2y}{28}=\dfrac{5z}{50}=\dfrac{3x-2y+5z}{63-28+50}=\dfrac{-30}{85}\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{30}{85}.21=-\dfrac{126}{17}\\y=-\dfrac{30}{85}.14=-\dfrac{84}{17}\\z=-\dfrac{30}{85}.10=-\dfrac{60}{17}\end{matrix}\right.\)
Em có ghi nhầm đề đâu ko mà kết quả xấu quá

\(A=\dfrac{3^{2022}+2}{3^{2022}-1}=\dfrac{3^{2022}-1+3}{3^{2022}-1}=1+\dfrac{3}{3^{2022}-1}\)
\(B=\dfrac{3^{2022}}{3^{2022}-3}=\dfrac{3^{2022}-3+3}{3^{2022}-3}=1+\dfrac{3}{3^{2022}-3}\)
Vì \(3^{2022}-1>3^{2022}-3\)
nên \(\dfrac{3}{3^{2022}-1}< \dfrac{3}{3^{2022}-3}\)
=>\(1+\dfrac{3}{3^{2022}-1}< 1+\dfrac{3}{2^{2022}-3}\)
=>A<B

Với các số dương \(a;b;n\) sao cho \(a>b\) ta luôn có: \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Thật vậy, do \(a>b\Rightarrow an>bn\Rightarrow ab+an>ab+bn\)
\(\Rightarrow a\left(b+n\right)>b\left(a+n\right)\)
\(\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Áp dụng:
Do \(3^{2022}>3^{2022}-3>0\) và \(2>0\) nên:
\(\dfrac{3^{2022}}{3^{2022}-3}>\dfrac{3^{2022}+2}{3^{2022}-3+2}\Rightarrow\dfrac{3^{2022}}{3^{2022}-3}>\dfrac{3^{2022}+2}{3^{2022}-1}\)
Vậy \(B>A\)

Gọi cạnh khi tăng lên là a+5
Gọi cạnh khi chx tăng là b
Theo bài:
(a+5).b-ab=120
ab+5b-ab=120
5b=120
=>b=24
=>bn cho thiếu
mk là sai là lại nè
Gọi cạnh khi tăng là:a+5
Cạnh khi chx tăng là a
Theo bài
(a+5)xa-aa=120
aa+5a-aa=120
5a=120
a=24
=>diện tích hình vuông là
24x24=576

a: Xét ΔAEH vuông tại E và ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
b: Ta có: ΔAEH vuông tại E
=>\(EH^2+EA^2=AH^2\)
=>\(EH^2=10^2-6^2=64=8^2\)
=>EH=8(cm)
Xét ΔAHE có AM là phân giác
nên \(\dfrac{MH}{AH}=\dfrac{ME}{AE}\)
=>\(\dfrac{MH}{10}=\dfrac{ME}{6}\)
=>\(\dfrac{MH}{5}=\dfrac{ME}{3}\)
mà MH+ME=EH=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MH}{5}=\dfrac{ME}{3}=\dfrac{MH+ME}{5+3}=\dfrac{8}{8}=1\)
=>MH=5(cm); ME=3(cm)
c: Xét ΔHEC có HN là phân giác
nên \(\dfrac{EN}{NC}=\dfrac{EH}{HC}\left(1\right)\)
Xét ΔAHE có AM là phân giác
nên \(\dfrac{EM}{MH}=\dfrac{EA}{AH}\left(2\right)\)
Xét ΔEHA vuông tại E và ΔHCA vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔEHA~ΔHCA
=>\(\dfrac{EA}{HA}=\dfrac{EH}{HC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{EM}{MH}=\dfrac{EN}{NC}\)
Xét ΔEHC có \(\dfrac{EM}{MH}=\dfrac{EN}{NC}\)
nên MN//HC
=>MN//BC
mà AH\(\perp\)BC
nên HA\(\perp\)MN
Xét ΔAHN có
NM,HE là các đường cao
NM cắt HE tại M
Do đó: M là trực tâm của ΔAHN
=>AM\(\perp\)HN

Lời giải:
Độ dài cạnh sân trường ban đầu:
$120:5=24$ (m)
Lúc đầu diện tích sân trường là:
$24\times 24=576$ (m2)

\(P=\left(a^2+b\right)-\left(2a^2+b\right)+2\left(ab+2021b\right)\)
\(=a^2+b-2a^2-b+2ab+2\cdot2021b\)
\(=-a^2+2ab+2\cdot b\left(a-2b\right)\)
\(=-a^2+2ab+2ba-4b^2\)
\(=-\left(a^2-4ab+4b^2\right)\)
\(=-\left(a-2b\right)^2=-2021^2\)
Đặt \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2024}}\)
=>\(2A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{2023}}\)
=>\(2A-A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{2023}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2024}}\)
=>\(A=1-\dfrac{1}{2^{2024}}\)
\(223-x\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2024}}\right):\left(1-\dfrac{1}{2^{2024}}\right)=23\)
=>\(223-x\left(1-\dfrac{1}{2^{2024}}\right):\left(1-\dfrac{1}{2^{2024}}\right)=23\)
=>223-x=23
=>x=200