Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{27}{8}-\dfrac{7}{3}+\dfrac{4}{3}-2\)
\(=\dfrac{27}{8}-1-2\)
\(=\dfrac{27}{8}-3=\dfrac{3}{8}\)
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian dự kiến ban đầu là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian đi nửa quãng đường ban đầu là \(\dfrac{x}{2}:40=\dfrac{x}{80}\left(giờ\right)\)
vận tốc trên nửa quãng đường còn lại là 40+10=50(km/h)
Thời gian đi nửa quãng đường còn lại là \(\dfrac{x}{2}:50=\dfrac{x}{100}\left(giờ\right)\)
Tổng thời gian là 11h30p-6h30p-30p=4h30p=4,5(giờ)
Theo đề, ta có phương trình:
\(\dfrac{x}{80}+\dfrac{x}{100}=4,5\)
=>\(\dfrac{9x}{400}=4,5\)
=>\(9x=400\cdot4,5=1800\)
=>\(x=\dfrac{1800}{9}=200\left(nhận\right)\)
vậy: Quãng đường AB là 200km
Số dân cuối năm 2012 là:
\(93750\cdot\left(1+1,6\%\right)=95250\left(người\right)\)
Số dân cuối năm 2013 là:
\(95250\left(1+1,6\%\right)=96774\left(người\right)\)
Số người tăng thêm là:
96774-93750=3024(người)
Thời gian thực tế xe ô tô đi là:
11h30p-7h45p-30p=11h-7h45p=3h15p
a: \(P=\dfrac{x}{x-2}+\dfrac{2-x}{x+2}+\dfrac{8-6x}{x^2-4}\)
\(=\dfrac{x}{x-2}-\dfrac{x-2}{x+2}+\dfrac{8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)-\left(x-2\right)^2+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x-x^2+4x-4+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{x^2-4}\)
b: Thay x=3 vào P, ta được:
\(P=\dfrac{4}{3^2-4}=\dfrac{4}{5}\)
Thay x=-1/2 vào P, ta được:
\(P=\dfrac{4}{\left(-\dfrac{1}{2}\right)^2-4}=\dfrac{4}{\dfrac{1}{4}-4}=4:\dfrac{-15}{4}=\dfrac{-16}{15}\)
c: Để P là số nguyên thì \(4⋮x^2-4\)
=>\(x^2-4\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x^2\in\left\{5;3;6;2;8;0\right\}\)
mà x nguyên
nên x^2=0
=>x=0(nhận)
Vì số chia là bé nhất nên số chia là: 5 + 1 = 6
Số bị chia là: 9 x 6 + 5 = 59
Đáp số: Số chia 6; số bị chia 59
Gọi thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là x(ngày) và y(ngày)
(ĐK: x>0; y>0)
Trong 1 ngày, người 1 làm được \(\dfrac{1}{x}\left(côngviệc\right)\)
Trong 1 ngày, người 2 làm được \(\dfrac{1}{y}\left(côngviệc\right)\)
Trong 1 ngày, hai người làm được \(\dfrac{1}{4}\left(côngviệc\right)\)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Trong 2 ngày, người 1 làm được \(\dfrac{2}{x}\)(công việc)
Trong 2+6=8 ngày, người 2 làm được \(\dfrac{8}{y}\)(công việc)
Vì làm được 2 ngày thì người 1 chuyển đi, người 2 làm tiếp trong 6 ngày thì xong công việc nên ta có: \(\dfrac{2}{x}+\dfrac{8}{y}=1\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{2}{x}+\dfrac{8}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{2}\\\dfrac{2}{x}+\dfrac{8}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{6}{y}=-\dfrac{1}{2}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\\dfrac{1}{x}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(nhận)
Vậy: thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là 6 ngày và 12 ngày
Giải:
Trong một ngày hai người cùng làm được:
1 : 4 = \(\dfrac{1}{4}\) (công việc)
Hai ngày hai người cùng làm được:
\(\dfrac{1}{4}\) x 2 = \(\dfrac{1}{2}\) (công việc)
Trong 6 ngày người thứ hai làm một mình được:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (công việc)
Trong một ngày người thứ hai làm một mình được:
\(\dfrac{1}{2}\) : 6 = \(\dfrac{1}{12}\) (công việc)
Trong một ngày người thứ nhất làm một mình được:
\(\dfrac{1}{4}\) - \(\dfrac{1}{12}\) = \(\dfrac{1}{6}\) (công việc)
Người thứ nhất làm một mình sẽ hoàn thành công việc sau:
1 : \(\dfrac{1}{6}\) = 6 (ngày)
Kết luận: người thứ nhất làm một mình sẽ xong công việc sau 6 ngày
Số có số hàng chục lớn hơn số hàng trăm là:
563
Chọn b.563
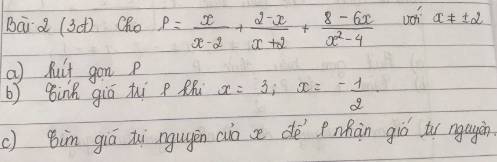
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
c: ta có: \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
d: ta có: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
=>DC>DA