
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔADB vuông tại D và ΔADE vuông tại D có
AD chung
DB=DE
Do đó: ΔADB=ΔADE
=>AB=AE
=>ΔABE cân tại A
b: Gọi H là giao điểm của CK và AD
Xét ΔAHC có
CD,AK là các đường cao
CD cắt AK tại E
Do đó: E là trực tâm của ΔAHC
=>HE\(\perp\)AC
mà EF\(\perp\)AC
nên H,E,F thẳng hàng
=>AD,EF,CK đồng quy

a: Xét ΔDKE và ΔDHF có
DK=DH
\(\widehat{KDE}\) chung
DE=DF
Do đó: ΔDKE=ΔDHF
=>KE=HF
b: Ta có: ΔDKE=ΔDHF
=>\(\widehat{DHF}=\widehat{DKE};\widehat{DEK}=\widehat{DFH}\)
Ta có: \(\widehat{DHF}+\widehat{EHF}=180^0\)(hai góc kề bù)
\(\widehat{DKE}+\widehat{FKE}=180^0\)(hai góc kề bù)
mà \(\widehat{DHF}=\widehat{DKE}\)
nên \(\widehat{EHF}=\widehat{FKE}\)
Ta có: DH+HE=DE
DK+KF=DF
mà DH=DK và DE=DF
nên HE=KF
Xét ΔOHE và ΔOKF có
\(\widehat{OHE}=\widehat{OKF}\)
HE=KF
\(\widehat{OEH}=\widehat{OFK}\)
Do đó: ΔOHE=ΔOKF
c: Ta có: ΔOHE=ΔOKF
=>OE=OF
=>O nằm trên đường trung trực của EF(1)
Ta có: DE=DF
=>D nằm trên đường trung trực của EF(2)
Từ (1),(2) suy ra DO là đường trung trực của EF
=>DO\(\perp\)EF

\(\dfrac{x^5+5x^3-3x^4-2x^2+3x-6}{x^2-3x+5}\)
\(=\dfrac{x^5-3x^4+5x^3-2x^2+6x-10-3x+4}{x^2-3x+5}\)
\(=\dfrac{x^3\left(x^2-3x+5\right)-2\left(x^2-3x+5\right)-3x+4}{x^2-3x+5}\)
\(=x^3-2+\dfrac{-3x+4}{x^2-3x+5}\)

a: -526,8<0
0<0,65
Do đó: -526,8<0,65
b: 6,45>0
0>-3,273
Do đó 6,45>-3,273
c: 7,78<9,56
=>-7,78>-9,56
d: 0,789>0,356
=>-0,789<-0,356

\(P\left(1\right)=1^3-2\cdot a\cdot1+a^2=a^2-2a+1\)
\(Q\left(3\right)=3^2+\left(3a+1\right)\cdot3+a^2=a^2+9a+12\)
P(1)=Q(3)
=>\(a^2+9a+12=a^2-2a+1\)
=>11a=-11
=>a=-1

x+y-3=0
=>x+y=3
\(M\left(x\right)=x^3+x^2y-3x^2-xy-y^2+4y+x+2020\)
\(=x^2\left(x+y\right)-3x^2-y\left(x+y\right)+4y+x+2020\)
\(=3x^2-3x^2-3y+4y+x+2020\)
=x+y+2020
=3+2020
=2023

a) \(P\left(x\right)=x^5-2x^4+3x^2-x+2;Q\left(x\right)=x^4-2x^3+x-5\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)+\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2+x^4-2x^3+x-5\)
\(=x^5+\left(-2x^4+x^4\right)-2x^3+3x^2+\left(-x+x\right)+\left(2-5\right)\)
\(=x^5-x^4-2x^3+3x^2-3\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)-\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2-x^4+2x^3-x+5\)
\(=x^5+\left(-2x^4-x^4\right)+2x^3+3x^2+\left(-x-x\right)+\left(2+5\right)\)
\(=x^5-3x^4+2x^3+3x^2-2x+7\)
b) \(P\left(x\right)=x^4+3x^5-x^2-4;Q\left(x\right)=x^4-x^2-3x^3+x\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)+\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4+x^4-x^2-3x^3+x\)
\(=3x^5+\left(x^4+x^4\right)-3x^3+\left(-x^2-x^2\right)+x-4\)
\(=3x^5+2x^4-3x^3-2x^2+x-4\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)-\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4-x^4+x^2+3x^3-x\)
\(=3x^5+\left(x^4-x^4\right)+3x^3+\left(-x^2+x^2\right)-x-4\)
\(=3x^5+3x^3-x-4\)
\(\text{#}Toru\)



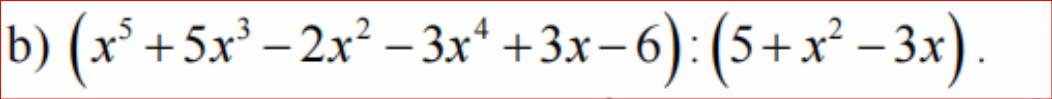

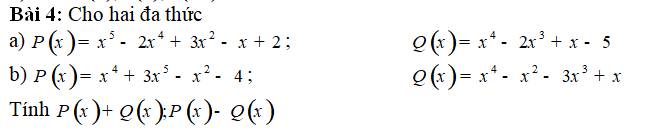

a: Xét ΔEDN và ΔEFN có
ED=EF
\(\widehat{DEN}=\widehat{FEN}\)
EN chung
Do đó: ΔEDN=ΔEFN
=>ND=NF
=>ΔNDF cân tại N
b: ΔEDN=ΔEFN
=>\(\widehat{EDN}=\widehat{EFN}\)
=>\(\widehat{EFN}=90^0\)
=>NF\(\perp\)FE