7^2020 : 2021 có số dư là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(2x^4-21^3+34x^2+105x+50=0\)
\(\Leftrightarrow2x^4-12x^3-10x^2-9x^3+54x^2+45x-10x^2+60x+50=0\)
\(\Leftrightarrow2x^2\left(x^2-6x-5\right)-9x\left(x^2-6x-5\right)-10\left(x^2-6x-5\right)=0\)
\(\Leftrightarrow\left(x^2-6x-5\right)\left(2x^2-9x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-6x-5=0\\2x^2-9x-10=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3+\sqrt{14}\\x=3-\sqrt{14}\\x=\dfrac{9+\sqrt{161}}{4}\\x=\dfrac{9-\sqrt{161}}{4}\end{matrix}\right.\)

Lời giải:
$x^2+x-12=0$
$\Leftrightarrow (x^2-3x)+(4x-12)=0$
$\Leftrightarrow x(x-3)+4(x-3)=0$
$\Leftrightarrow (x-3)(x+4)=0$
$\Leftrightarrow x-3=0$ hoặc $x+4=0$
$\Leftrightarrow x=3$ hoặc $x=-4$

Khi đó, ADAD là đường trung tuyến của tam giác ABCABC.
Vì GG là trọng tâm của tam giác ABCABC nên điểm GG nằm trên cạnh ADAD.
Ta có AGAD=23ADAG=32 hay AG=23ADAG=32AD.
Vì MGMG // ABAB, theo định lí Thalès, ta suy ra: AGAD=BMBD=23ADAG=BDBM=32.
Ta có BD=CDBD=CD (vì DD là trung điểm của cạnh BCBC) nên BMBC=BM2BD=22.3=13BCBM=2BDBM=2.32=31.
Do đó BM=13BCBM=31BC (đpcm).

A B C D F E
Ta có DE//AC \(\Rightarrow\dfrac{AE}{AB}=\dfrac{CD}{BC}\) (Talet)
Ta có DF//AB \(\Rightarrow\dfrac{AF}{AC}=\dfrac{BD}{BC}\) (Talet)
\(\Rightarrow\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD}{BC}+\dfrac{BD}{BC}=\dfrac{BC}{BC}=1\left(dpcm\right)\)

a)
\(\dfrac{x^3-8}{5x+10}.\dfrac{x^2+4x}{x^2+2x+4}=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{5\left(x+2\right)}.\dfrac{x\left(x+4\right)}{x^2+2x+4}\\ =\dfrac{\left(x-2\right).\left(x^2+4x\right)}{5x+10}\\ =\dfrac{x^3+4x^2-2x^2-8x}{5x+10}\\ =\dfrac{x^3+2x^2-8x}{5x+10}\)
b)
\(=\dfrac{\left(x-6\right)\left(x+6\right)}{2x+10}.-\dfrac{3}{x-6}\\ =\dfrac{-3\left(x+6\right)}{2x+10}\\ =\dfrac{-3x-18}{2x+10}\)
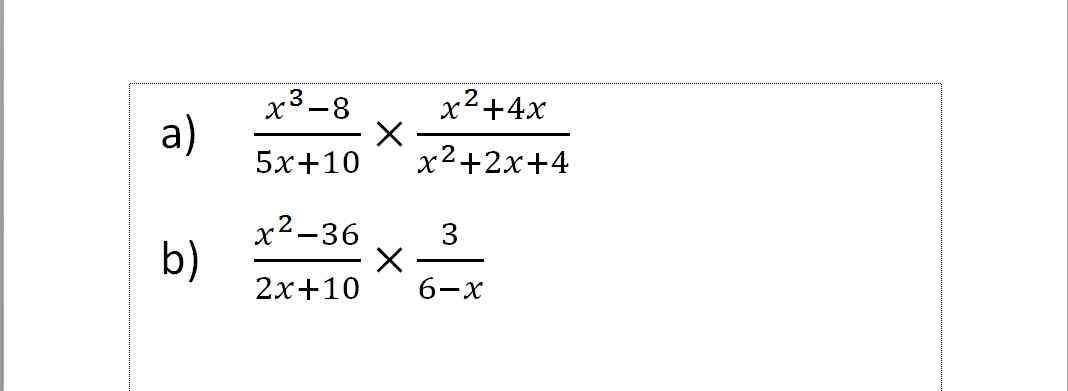
.