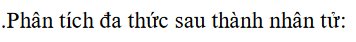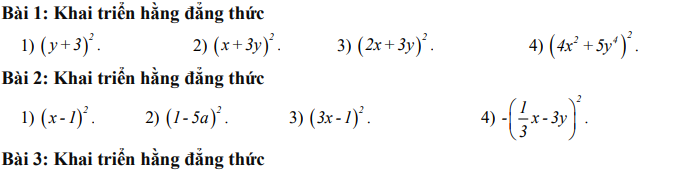Cho tam giác ABC có 3 đường cao AD, BE, CF cắt nhau tại H. Gọi K,M,N lần lượt là trực tâm tam giác AEF, BFD,CDE. Chứng minh rằng tam giác KMN bằng tam giác DEF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để tổng của M với đa thức \(x^2-2xy+y^2-2xz+z^2\) không chứa biến x thì \(M+x^2-2xy+y^2-2xz+z^2=y^2+z^2\)
=>\(M+x^2-2xy-2xz=0\)
=>\(M=-x^2+2xy+2xz\)

\(a,A=x^2+y^2+2x-6y-2\\ =\left(x^2+2x+1\right)+\left(y^2-6y+9\right)-12\\ =\left(x+1\right)^2+\left(y-3\right)^2-12\)
Ta có:
`(x+1)^2>=0` với mọi x
`(y-3)^2>=0` với mọi y
`=>A=(x+1)^2+(y-3)^2-12>=-12` với mọi x,y
Dấu "=" xảy ra: `x+1=0` và `y-3=0`
`<=>x=-1` và `y=3`
\(b,B=5x^2+y^2+z^2+4xy+2xz\\ =\left(4x^2+4xy+y^2\right)+\left(x^2+2xz+z^2\right)\\ =\left(2x+y\right)^2+\left(x+z\right)^2\)
Ta có:
`(2x+y)^2>=0` với mọi x,y
`(x+z)^2>=0` với mọi x,z
`=>B=(2x+y)^2+(x+z)^2>=0`
Dấu "=" xảy ra: `2x+y=0` và `x+z=0`
`<=>2x=-y=-2z`
\(c,C=2x^2+y^2+2xy-8x+2024\\ =\left(x^2+2xy+y^2\right)+\left(x^2-8x+16\right)+2008\\ =\left(x+y\right)^2+\left(x-4\right)^2+2008\)
Ta có:
`(x+y)^2>=0` với mọi x,y
`(x-4)^2>=0` với mọi x
`=>C=(x+y)^2+(x-4)^2+2008>=2008`
Dấu "=" xảy ra:
`x+y=0` và `x-4=0`
`<=>x=4` và `y=-4`
\(d,D=x^2-2xy+3y^2-2x+1997\\ =\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-2y+\dfrac{1}{2}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y^2-y+\dfrac{1}{4}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{3991}{2}\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-1/2)^2>=0` với mọi y
`=>D=(-x+y+1)^2+2(y-1/2)^2+3991/2>=3991/2`
Dấu "=" xảy ra: `-x+y+1=0` và `y-1/2=0`
`<=>y=1/2` và `x=3/2`

\(5,8a^3\left(a-b\right)-27\left(a-b\right)\\ =\left(a-b\right)\left(8a^3-27\right)\\ =\left(a-b\right)\left(2a-3\right)\left(4a^2+6a+9\right)\\ 6,27\left(a+b\right)-a^3\left(a+b\right)\\ =\left(a+b\right)\left(27-a^3\right)\\ =\left(a+b\right)\left(3-a\right)\left(9+3a+a^2\right)\\ 7,8a^3\left(2a-3b\right)+27\left(2a-3b\right)\\ =\left(2a-3b\right)\left(8a^3+27\right)\\ =\left(2a-3b\right)\left(2a+3\right)\left(4a^2-6a+9\right)\)

Xét tứ giác MNPQ ta có:
\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^o\) (tổng các góc trong tam giác)\
\(\widehat{M}:\widehat{N}:\widehat{P}:\widehat{Q}=1:2:3:4\\ =>\dfrac{\widehat{M}}{1}=\dfrac{\widehat{N}}{2}=\dfrac{\widehat{P}}{3}=\dfrac{\widehat{Q}}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{\widehat{M}}{1}=\dfrac{\widehat{N}}{2}=\dfrac{\widehat{P}}{3}=\dfrac{\widehat{Q}}{4}=\dfrac{\widehat{M}+\widehat{N}+\widehat{Q}+\widehat{Q}}{1+2+3+4}=\dfrac{360^o}{10}=36^o\\ =>\widehat{M}=36^o\\ =>\dfrac{\widehat{N}}{2}=36^o=>\widehat{N}=72^o\\ =>\dfrac{\widehat{P}}{3}=36^o=>\widehat{P}=108^o\\ =>\dfrac{\widehat{Q}}{4}=36^o=>\widehat{Q}=144^o\)
Vì: \(\widehat{M}+\widehat{Q}=36^o+144^o=180^o\) => MN//PQ => MNPQ là hình thang

Bài 1:
\(1,\left(y+3\right)^2\\ =y^2+2\cdot y\cdot3+3^2\\ =y^2+6y+9\\ 2,\left(x+3y\right)^2\\ =x^2+2\cdot x\cdot3y+\left(3y\right)^2\\ =x^2+6xy+9y^2\\ 3,\left(2x+3y\right)^2\\ =\left(2x\right)^2+3\cdot2x\cdot3y+\left(3y\right)^2\\ =4x^2+18xy+9y^2\\ 4,\left(4x^2+5y^4\right)\\ =\left(4x^2\right)^2+2\cdot4x^2\cdot5y^4+\left(5y^4\right)^2\\ =16x^4+40x^2y^4+25y^8\)
Bài 2:
\(1,\left(x-1\right)^2\\ =x^2-2\cdot x\cdot1+1^2\\ =x^2-2x+1\\ 2,\left(1-5a\right)^2\\ =1^2-2\cdot1\cdot5a+\left(5a\right)^2\\ =1-10a+25a^2\\ 3,\left(3x-1\right)^2\\ =\left(3x\right)^2-2\cdot3x\cdot1+1^2\\ =9x^2-6x+1\\ 4,-\left(\dfrac{1}{3}x-3y\right)^2\\ =-\left[\left(\dfrac{1}{3}x\right)^2-2\cdot\dfrac{1}{3}x\cdot3y+\left(3y\right)^2\right]\\ =-\left(\dfrac{1}{9}x^2-2xy+9y^2\right)\\ =-\dfrac{1}{9}x^2+2xy-9y^2\)

Gọi chiều dài màn hình là `x` (cm)
ĐK: `x>0`
Đổi: 17inch ≃ 43,18 (cm)
Chiều cao màn hình là: `5/8x(cm)`
Áp dụng định lý Pythagore ta có:
\(x^2+\left(\dfrac{5}{8}x\right)^2=43,18^2\\ < =>x^2+\dfrac{25}{64}x^2=1864,5124\\ < =>\dfrac{79}{64}x^2=1864,5124\\ < =>x^2\approx1510,4\\ < =>x\approx38,9\left(cm\right)\left(x>0\right)\)
=> Chiều cao của màn hình là: `5/8*38,9≃24,3(cm)`
Vậy:
Gọi x (cm) là chiều rộng màn hình (x > 0)
Chiều dài màn hình là:
 Đổi 17 inch ≈ 43,2 cm
Đổi 17 inch ≈ 43,2 cm
 Theo đề bài, ta có phương trình:
Theo đề bài, ta có phương trình:
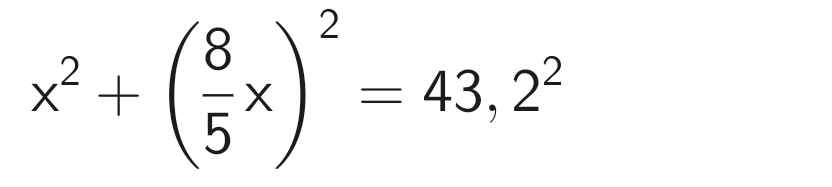
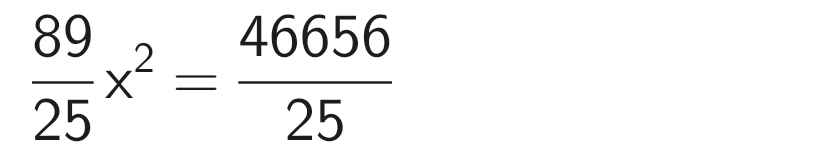
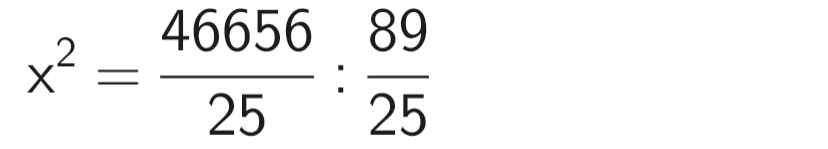

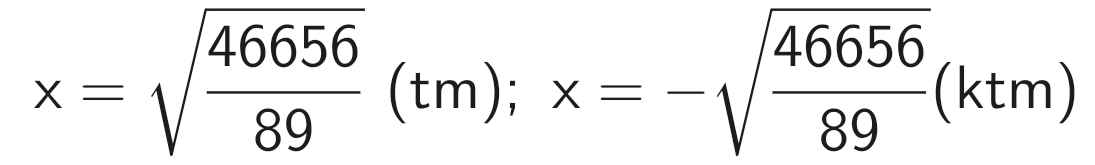
⇒ x ≈ 22,9 (cm)
Vậy chiều rộng màn hình là 22,9 cm, chiều dài màn hình là 22,9.1,6 ≈ 36,6 cm
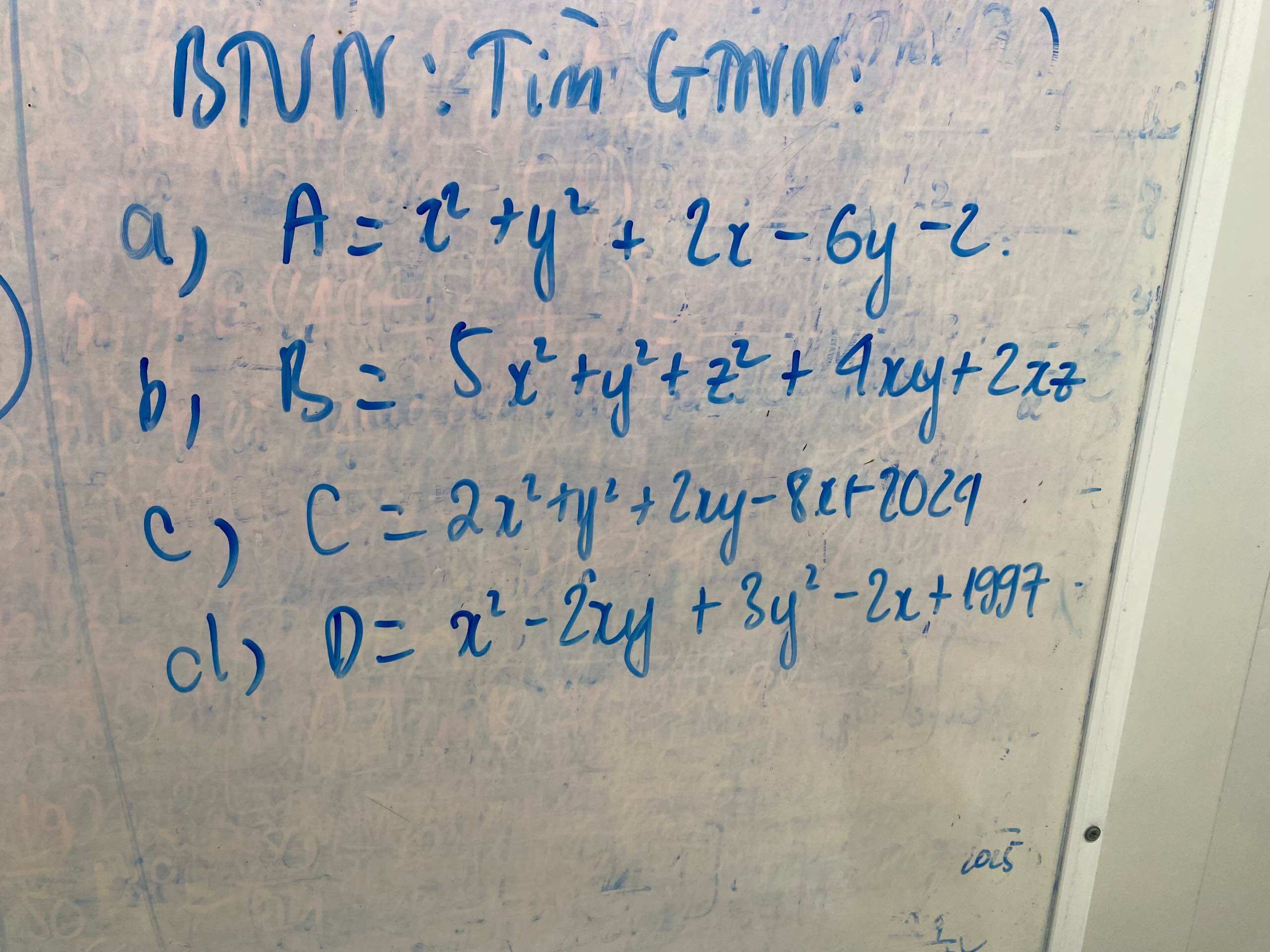
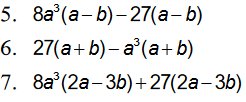 Giúp mik với ạ
Giúp mik với ạ