Hai công nhân phải làm 1 số dụng cụ như nhau trong cùng một thời gian. Người thứ nhất làm vượt định mức mỗi ngày 3 dụng cụ nên làm xong công việc trước thời hạn 2 ngày. Người thứ hai làm kém định mức mỗi ngày 3 dụng cụ nên làm lâu hơn thời hạn 3 ngày. Tính số dụng cụ được giao.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left(x+5\right)\left(x-1\right)=2x\left(x-1\right)\)
=>\(2x\left(x-1\right)-\left(x+5\right)\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x-x-5\right)=0\)
=>(x-1)(x-5)=0
=>\(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
b: \(3\left(x-1\right)\left(2x-1\right)=5\left(x+8\right)\left(x-1\right)\)
=>\(\left(x-1\right)\left(6x-3\right)-\left(x-1\right)\left(5x+40\right)=0\)
=>\(\left(x-1\right)\left(6x-3-5x-40\right)=0\)
=>(x-1)(x-43)=0
=>\(\left[{}\begin{matrix}x=1\\x=43\end{matrix}\right.\)
c: \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)
=>\(\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)
=>\(\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)
=>(x-3)(x-4)(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=3\\x=4\\x=1\\x=2\end{matrix}\right.\)
d: \(x^3-5x^2+6x=0\)
=>\(x\left(x^2-5x+6\right)=0\)
=>x(x-2)(x-3)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\\x=3\end{matrix}\right.\)
e: \(\left(x+3\right)\left(x-5\right)+\left(x+3\right)\left(3x-4\right)=0\)
=>(x+3)(x-5+3x-4)=0
=>(x+3)(4x-9)=0
=>\(\left[{}\begin{matrix}x=-3\\x=\dfrac{9}{4}\end{matrix}\right.\)
f: \(\left(x+7\right)\left(3x-1\right)=49-x^2\)
=>\(\left(x+7\right)\left(3x-1\right)+x^2-49=0\)
=>(x+7)(3x-1)+(x-7)(x+7)=0
=>(x+7)(3x-1+x-7)=0
=>(x+7)(4x-8)=0
=>\(\left[{}\begin{matrix}x=-7\\x=2\end{matrix}\right.\)
g: \(3x^2-7x+4=0\)
=>\(3x^2-3x-4x+4=0\)
=>(x-1)(3x-4)=0
=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)
h: \(2x^3+3x^2-32x=48\)
=>\(2x^3+3x^2-32x-48=0\)
=>\(x^2\left(2x+3\right)-16\left(2x+3\right)=0\)
=>\(\left(2x+3\right)\left(x^2-16\right)=0\)
=>(2x+3)(x-4)(x+4)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=4\\x=-4\end{matrix}\right.\)
a) (x + 5)(x - 1) = 2x(x - 1)
(x + 5)(x - 1) - 2x(x - 1) = 0
(x - 1)(x + 5 - 2x) = 0
(x - 1)(5 - x) = 0
x - 1 = 0 hoặc 5 - x = 0
*) x - 1 = 0
x = 1
*) 5 - x = 0
x = 5
Vậy S = {1; 5}
b) 3(x - 1)(2x - 1) = 5(x + 8)(x - 1)
(x - 1)(6x - 3) = (5x + 40)(x - 1)
(x - 1)(6x - 3) - (5x + 40)(x - 1) = 0
(x - 1)(6x - 3 - 5x - 40) = 0
(x - 1)(x - 43) = 0
x - 1 = 0 hoặc x - 43 = 0
*) x - 1 = 0
x = 1
*) x - 43 = 0
x = 43
Vậy S = {1; 43}
c) (x² - 5x + 7)² - (2x - 5)² = 0
(x² - 5x + 7 - 2x + 5)(x² - 5x + 7 + 2x - 5) = 0
(x² - 7x + 12)(x² - 3x + 2) = 0
x² - 7x + 12 = 0 hoặc x² - 3x + 2 = 0
*) x² - 7x + 12 = 0
x² - 3x - 4x + 12 = 0
(x² - 3x) - (4x + 12) = 0
x(x - 3) - 4(x - 3) = 0
(x - 3)(x - 4) = 0
x - 3 = 0 hoặc x - 4 = 0
+) x - 3 = 0
x = 3
+) x - 4 = 0
x = 4
*) x² - 3x + 2 = 0
x² - x - 2x + 2 = 0
(x² - x) - (2x - 2) = 0
x(x - 1) - 2(x - 1) = 0
(x - 1)(x - 2) = 0
x - 1 = 0 hoặc x - 2 = 0
+) x - 1 = 0
x = 1
+) x - 2 = 0
x = 2
Vậy S = {1; 2; 3; 4}
d) x³ - 5x² + 6x = 0
x(x² - 5x + 6) = 0
x = 0 hoặc x² - 5x + 6 = 0
*) x² - 5x + 6 = 0
x² - 2x - 3x + 6 = 0
(x² - 2x) - (3x - 6) = 0
x(x - 2) - 3(x - 2) = 0
(x - 2)(x - 3) = 0
x - 2 = 0 hoặc x - 3 = 0
+) x - 2 = 0
x = 2
+) x - 3 = 0
x = 3
Vậy S = {0; 2; 3}

a: 5-(x-6)=4(2x-3)
=>8x-12=5-x+6
=>8x-12=-x+11
=>9x=23
=>\(x=\dfrac{23}{9}\)
b: \(3-4x+24+6x=x+27+3x\)
=>\(4x+27=2x+27\)
=>2x=0
=>x=0
c: \(\left(x+5\right)\left(x-1\right)=2x\left(x-1\right)\)
=>\(2x\left(x-1\right)-\left(x+5\right)\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x-x-5\right)=0\)
=>(x-1)(x-5)=0
=>\(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
d: \(5\left(3x-2\right)-4\left(5-3x\right)=1\)
=>\(15x-10-20+12x=1\)
=>27x=1+30=31
=>\(x=\dfrac{31}{27}\)

\(x^{2020}\) + 8\(x^{2008}\) = 0
\(x^{2008}\).(\(x^{12}\) + 8) = 0
\(x^{12}\) ≥ 0 ∀ \(x\) ⇒ \(x^{12}\) + 8 ≥ 8 ∀ \(x\)
\(x^{2008}\)(\(x^{12}\) + 8) = 0 ⇔ \(x^{2008}\) = 0 ⇒ \(x=0\)
Kết luận \(x=0\)

Gọi vận tốc thật của thuyền là x(km/h)
Đổi \(1h10p=\dfrac{7}{6}\left(giờ\right);1h30p=1,5\left(giờ\right)\)
Vận tốc lúc xuôi dòng là x+2(km/h)
vận tốc lúc ngược dòng là x-2(km/h)
Độ dài quãng đường lúc xuôi dòng là \(\dfrac{7}{6}\left(x+2\right)\)(km)
Độ dài quãng đường lúc ngược dòng là 1,5(x-2)(km)
Do đó, ta có phương trình:
\(\dfrac{7}{6}\left(x+2\right)=1.5\left(x-2\right)\)
=>\(\dfrac{7}{6}x+\dfrac{7}{3}=1,5x-3\)
=>\(x\left(\dfrac{7}{6}-1,5\right)=-3-\dfrac{7}{3}\)
=>\(x\cdot\dfrac{-1}{3}=\dfrac{-16}{3}\)
=>x=16(nhận)
Vậy: Độ dài quãng đường là 1,5(16-2)=21(km)
Giải:
1 giờ 10 phút = \(\dfrac{7}{6}\) giờ; 1 giờ 30 phút = 1,5 giờ
Gọi quãng sông AB là \(x\) (km); \(x>0\)
Vận tốc ca nô xuôi dòng là: \(x\) : \(\dfrac{7}{6}\) = \(\dfrac{6}{7}\)\(x\) (km)
Vận tốc ca nô ngược dòng là: \(x\) : 1,5 = \(\dfrac{2}{3}x\)
Theo bài ra ta có: \(\dfrac{6}{7}x\) - \(\dfrac{2}{3}x\) = 2 x 2
\(\dfrac{4}{21}\)\(x\) = 4
\(x\) = 4 : \(\dfrac{4}{21}\)
\(x\) = 21 (km)
Vậy quãng sông AB dài 21 km

Bài 4:
Bán kính hình tròn là:
\(0,25:2=0,125\left(dm\right)\)
bài 7:
a: 1m=10dm
Diện tích xung quanh của bể là:
\(\left(10+6,8\right)\cdot2\cdot7=14\cdot16,8=235,2\left(dm^2\right)\)
Diện tích kính dùng làm bể là:
\(235,2+10\cdot6,8=303,2\left(dm^2\right)\)
b: Thể tích nước tối đa đổ được vào bể là:
\(10\cdot6,8\cdot7=476\left(lít\right)\)
Bài 5:
Diện tích toàn phần của hình lập phương là:
\(105\cdot1,5=157,5\left(cm^2\right)\)

\(427\cdot4+427\cdot5+427\)
=427(4+5+1)
\(=427\cdot10=4270\)

a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AD=DC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AD=DC
Xét ΔADB và ΔAEC có
AD=AE
\(\widehat{DAB}\) chung
AB=AC
Do đó: ΔADB=ΔAEC
=>BD=CE
Xét ΔABC có
BD,CE là các đường trung tuyến
BD cắt CE tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BD;CG=\dfrac{2}{3}CE\)
mà BD=CE
nên BG=CG
Ta có: BG+GD=BD
CG+GE=CE
mà BG=CG và BD=CE
nên GD=GE
=>ΔGDE cân tại G
b: Xét ΔGBC có GB+GC>BC
=>\(\dfrac{2}{3}\left(BD+CE\right)>BC\)
=>\(BD+CE>\dfrac{3}{2}BC\)

a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB~ΔCAB
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
ΔAHB~ΔCAB
=>\(\dfrac{AH}{CA}=\dfrac{HB}{AB}=\dfrac{AB}{CB}\)
=>\(\dfrac{AH}{8}=\dfrac{HB}{6}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(AH=8\cdot\dfrac{3}{5}=4,8\left(cm\right);HB=6\cdot\dfrac{3}{5}=\dfrac{18}{5}=3,6\left(cm\right)\)
c: Ta có: \(\widehat{BHE}+\widehat{DHE}+\widehat{DHC}=180^0\)
=>\(\widehat{BHE}+\widehat{DHC}+90^0=180^0\)
=>\(\widehat{BHE}+\widehat{DHC}=90^0\)
mà \(\widehat{DHC}+\widehat{DHA}=\widehat{CHA}=90^0\)
nên \(\widehat{BHE}=\widehat{DHA}\)
Xét ΔBHE và ΔAHD có
\(\widehat{BHE}=\widehat{DHA}\)
\(\widehat{HBE}=\widehat{HAD}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔBHE~ΔAHD
Tìm các số nguyên x, y biết rằng: \(\dfrac{-10}{15}\)\(=\)\(\dfrac{\chi}{-9}\)\(=\)\(\dfrac{-8}{y}\)

\(\dfrac{-10}{15}=\dfrac{x}{-9}=\dfrac{-8}{y}\)
=>\(\dfrac{2}{3}=\dfrac{x}{9}=\dfrac{8}{y}\)
=>\(\left\{{}\begin{matrix}x=2\cdot\dfrac{9}{3}=2\cdot3=6\\y=8\cdot\dfrac{3}{2}=4\cdot3=12\end{matrix}\right.\)
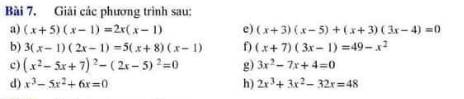
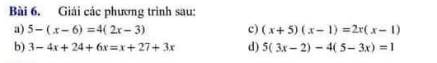


Gọi số dụng cụ mỗi ngày phải làm là x(dụng cụ), gọi số ngày phải hoàn thành là y(ngày)
(Điều kiện: \(x\in Z^+;y>0\))
Người thứ nhất làm vượt mức mỗi ngày 3 dụng cụ nên làm xong công việc sớm 2 ngày nên ta có:
(x+3)(y-2)=xy
=>xy-2x+3y-6=xy
=>-2x+3y=6(1)
Người thứ hai làm kém định mức mỗi ngày 3 dụng cụ nên hoàn thành lâu hơn 3 ngày nên ta có:
(x-3)(y+3)=xy
=>xy+3x-3y-9=xy
=>3x-3y=9
=>x-y=3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2x+3y=6\\x-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+3y=6\\2x-2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+3y+2x-2y=6+6\\x-y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=12\\x=y+3=15\end{matrix}\right.\left(nhận\right)\)
Số dụng cụ được giao là 12*15=180(dụng cụ)