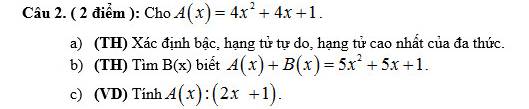
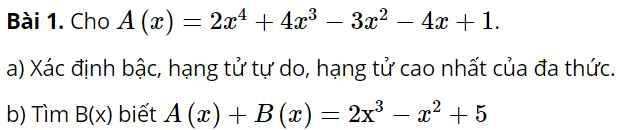
a: \(A\left(x\right)=-2x^5+3x^2-4x^5+x^6-2x^2-1\)

\(=x^6+\left(-2x^5-4x^5\right)+\left(3x^2-2x^2\right)-1\)

\(=x^6-6x^5+x^2-1\)

\(=-1+x^2-6x^5+x^6\)

\(B\left(x\right)=-x^6+3-2x-x^2+x^4-2x^6-x^2+4x^2-x^4\)

\(=\left(-x^6-2x^6\right)+\left(x^4-x^4\right)+\left(-x^2-x^2+4x^2\right)-2x+3\)

\(=-3x^6+2x^2-2x+3\)

\(=3-2x+2x^2-3x^6\)

b: \(A\left(x\right)=x^6-6x^5+x^2-1\)

Hệ số cao nhất là 1

Hệ số tự do là -1

Bậc là 6

\(B\left(x\right)=-3x^6+2x^2-2x+3\)

Bậc là 6

Hệ số cao nhất là -3

Hệ số tự do là 3

c: \(A\left(-1\right)=\left(-1\right)^6-6\cdot\left(-1\right)^5+\left(-1\right)^2-1\)

=1+6+1-1

=7

\(A\left(0\right)=0^6-6\cdot0^5+0^2-1=-1\)

\(A\left(1\right)=1^6-6\cdot1^5+1^2-1=1-6+1-1=-5\)

\(A\left(2\right)=2^6-6\cdot2^5+2^2-1=64-192+4-1=68-193=-125\)

d: A(0)=-1

=>x=0 không là nghiệm của A(x)

\(B\left(1\right)=-3\cdot1^6+2\cdot1^2-2\cdot1+3\)

=-3+2-2+3

=0

=>x=1 là nghiệm của B(x)

Gọi số vở lớp 7A,7B,7C quyên góp lần lượt là a(quyển),b(quyển),c(quyển)

(ĐIều kiện: \(a,b,c\in Z^+\))

Số vở lớp 7A;7B;7C quyên góp lần lượt tỉ lệ với 2;3;4

=>\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)

Tổng số vở 3 lớp quyên góp là 360 quyển nên a+b+c=360

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{360}{9}=40\)

=>\(a=40\cdot2=80;b=40\cdot3=120;c=40\cdot4=160\)

Vậy: số vở lớp 7A,7B,7C quyên góp lần lượt là 80(quyển),120(quyển),160(quyển)

a: Thể tích của chiếc hộp là:

\(22\cdot16\cdot18=6336\left(cm^2\right)\)

b: Diện tích xung quanh của hộp là:

\(\left(22+16\right)\cdot2\cdot18=1368\left(cm^2\right)\)

Diện tích bìa để làm hộp là:

1368+22x2x16=2072(cm²)

Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

=>\(\widehat{AIB}=\widehat{AIC}\)

mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)

nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)

=>AI\(\perp\)BC

a: Đặt P(x)=0

=>12-5x=0

=>5x=12

=>x=2,5

b: Đặt Q(y)=0

=>4y-3-5y=0

=>-y-3=0

=>y=-3

c: Đặt E(x)=0

=>\(4x^2-4=0\)

=>\(x^2=1\)

=>\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

d: Đặt H(x)=0

=>\(x^2+9=0\)

mà \(x^2+9>=9>0\forall x\)

nên \(x\in\varnothing\)

a: \(A\left(x\right)=4x^2+4x+1\)

bậc là 2

Hạng tử tự do là 1

Hạng tử cao nhất là 4x²

b: A(x)+B(x)=5x²+5x+1

=>\(B\left(x\right)=5x^2+5x+1-A\left(x\right)\)

=>\(B\left(x\right)=5x^2+5x+1-4x^2-4x-1=x^2+x\)

c: \(\dfrac{A\left(x\right)}{2x+1}=\dfrac{4x^2+4x+1}{2x+1}=\dfrac{\left(2x+1\right)^2}{2x+1}=2x+1\)

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có

BC chung

\(\widehat{EBC}=\widehat{DCB}\)

Do đó: ΔEBC=ΔDCB

b: Ta có: ΔEBC=ΔDCB

=>\(\widehat{ECB}=\widehat{DBC}\)

=>\(\widehat{HBC}=\widehat{HCB}\)

=>ΔHBC cân tại H

Xét ΔBHC có HB+HC>BC

=>BC<2BH

=>\(BH>\dfrac{BC}{2}\)

a: \(A\left(x\right)=2x^3-6x^2-5\left(x^2-2x-5\right)\)

\(=2x^3-6x^2-5x^2+10x+25\)

\(=2x^3-11x^2+10x+25\)

\(B\left(x\right)=x^3-3\left(x^3-2x^2-5x\right)\)

\(=x^3-3x^3+6x^2+15x\)

\(=-2x^3+6x^2+15x\)

b: \(A\left(x\right)=2x^3-11x^2+10x+25\)

Bậc là 2

Hệ số cao nhất là 2

Hệ số tự do là 25

c: A(x)-C(x)=B(x)

=>C(x)=A(x)-B(x)

\(=2x^3-11x^2+10x+25+2x^3-6x^2-15x\)

\(=4x^3-17x^2-5x+25\)

d: Đặt P(x)=0

=>B(x)+2x³=0

=>\(-2x^3+6x^2+15x+2x^3=0\)

=>\(6x^2+15x=0\)

=>3x(2x+5)=0

=>x(2x+5)=0

=>\(\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)

a: \(A\left(x\right)=2x^4+4x^3-3x^2-4x+1\)

bậc là 4

Hạng tử tự do là 1

Hạng tử cao nhất là \(2x^4\)

b: \(A\left(x\right)+B\left(x\right)=2x^3-x^2+5\)

=>\(B\left(x\right)=2x^3-x^2+5-A\left(x\right)\)

\(=2x^3-x^2+5-2x^4-4x^3+3x^2+4x-1\)

\(=-2x^4-2x^3+2x^2+4x+4\)