cho M là một điểm nằm trong góc xOy và khoảng cách từ M đến 2 cạnh Ox và Oy bằng nhau
a) nối OM . Hãy chỉ ra cặp tam giác bằng nhau trên hình vẽ
b) chứng minh △ OxM = △ OyM . Từ đó suy ra OM là tia phân giác của góc xOy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔABM=ΔCDM
b: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
HA=HE
Do đó: ΔBHA=ΔBHE
=>BA=BE
mà BA=CD(ΔMAB=ΔMCD)
nên BE=CD
c: Xét ΔAEC có
CH,EM là các đường trung tuyến
CH cắt EM tại K
Do đó: K là trọng tâm của ΔAEC
Xét ΔAEC có
K là trọng tâm
I là trung điểm của EC
Do đó: A,K,I thẳng hàng

áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{2}=\dfrac{c}{4}=\dfrac{a+b+c}{3+2+4}=\dfrac{45}{9}=5\)
=>\(a=5\cdot3=15;b=2\cdot5=10;c=4\cdot5=20\)

Vì mật khẩu là một số có 3 chữ số và mỗi chữ số đều là số lẻ, nên các chữ số lẻ có thể là 1, 3, 5, 7 hoặc 9. Điều này có nghĩa là mỗi chữ số trong mật khẩu có 5 lựa chọn khác nhau.
Do đó, tổng số mật khẩu có thể có là: 5×5×5=125
Giờ ta giả sử Nam chỉ nhấn một lần để mở cửa.
Để xác định xác suất mà Nam mở được cửa ngay lần nhấn đầu tiên, ta nhận thấy chỉ có một mật khẩu đúng trong số 125 mật khẩu có thể.
Vậy xác suất mà Nam mở được cửa từ lần nhấn đầu tiên là: 1/125
Như vậy, xác suất Nam bấm một lần mở được cửa là 1/125 hay khoảng 0.008 (0.8%).
Vì mật khẩu là một số có 3 chữ số và mỗi chữ số đều là số lẻ, nên các chữ số lẻ có thể là 1, 3, 5, 7 hoặc 9. Điều này có nghĩa là mỗi chữ số trong mật khẩu có 5 lựa chọn khác nhau.
Do đó, tổng số mật khẩu có thể có là: 5×5×5=125
Giờ ta giả sử Nam chỉ nhấn một lần để mở cửa.
Để xác định xác suất mà Nam mở được cửa ngay lần nhấn đầu tiên, ta nhận thấy chỉ có một mật khẩu đúng trong số 125 mật khẩu có thể.
Vậy xác suất mà Nam mở được cửa từ lần nhấn đầu tiên là: 1/125
Như vậy, xác suất Nam bấm một lần mở được cửa là 1/125 hay khoảng 0.008 (0.8%).

ta có 3/4 giờ = 0.75 giờ
Quãng đường bay được của chim ưng là s = v*t = (3/4)*96 = 0.75*96 = 72 (km)
Vậy...

a: \(A\left(x\right)=3x^3-4x^2+5x-7+3x+9\)
\(=3x^3-4x^2+\left(5x+3x\right)+\left(9-7\right)\)
\(=3x^3-4x^2+8x+2\)
bậc là 3
\(B\left(x\right)=5x^2-2x^3+6x-x^2-3x+20\)
\(=-2x^3+\left(5x^2-x^2\right)+\left(6x-3x\right)+20\)
\(=-2x^3+4x^2+3x+20\)
bậc là 3
b: \(A\left(x\right)=3x^3-4x^2+8x+2\)
=>Các hệ số là 3;-4;8;2
\(B\left(x\right)=-2x^3+4x^2+3x+20\)
=>Các hệ số là -2;4;3;20
c: \(A\left(2\right)=3\cdot2^3-4\cdot2^2+8\cdot2+2=24-16+16+2=26\)
d: \(P\left(-2\right)=\left(-2\right)^2-5\cdot\left(-2\right)+30\)
\(=4+10+30=44>0\)
=>x=-2 không là nghiệm của P(x)

(x-1)(6x+1) - (2x+1)(3x-5) = -10
<=> (6x2 + x - 6x - 1) - (6x2 - 10x + 3x - 5) = -10
<=> 6x2 + x - 6x - 1 - 6x2 + 10x - 3x + 5 = -10
<=> 2x + 4 = -10
<=> 2x = -14
<=> x = -7
Vậy x = -7
(x-1)(6x+1) - (2x+1)(3x-5) = -10
<=> (6x2 + x - 6x - 1) - (6x2 - 10x + 3x - 5) = -10
<=> 6x2 + x - 6x - 1 - 6x2 + 10x - 3x + 5 = -10
<=> 2x + 4 = -10
<=> 2x = -14
<=> x = -7
Vậy x = -7

Chứ m2 là đơn vị đo diện tích nha bạn, không thể đổi sang đơn vị đo thể tích là lít.

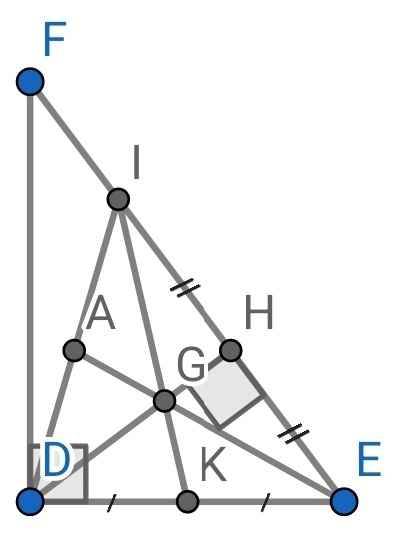
a) Xét hai tam giác vuông: ∆DHE và ∆DHI có:
DH là cạnh chung
HE = HI (gt)
⇒ ∆DHE = ∆DHI (hai cạnh góc vuông)
b) Do HE = HI (gt)
⇒ H là trung điểm của IE
⇒ DH là đường trung tuyến của ∆DEI
Do K là trung điểm của DE (gt)
⇒ IE là đường trung tuyến thứ hai của ∆DEI
Mà G là giao điểm của IK và DH (gt)
⇒ G là trọng tâm của ∆DEI
⇒ DG = 2/3 . DH
Gọi A là trung điểm của DI
Do G là trọng tâm của ∆DEI (cmt)
⇒ EG là đường trung tuyến thứ ba của ∆DEI
⇒ EG đi qua trung điểm A của DI
Em xem lại đề nhé. H, K ở đâu ra vậy em?