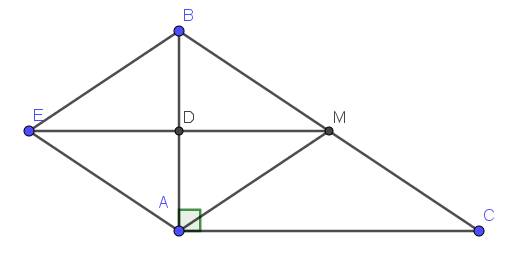
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH. Gọi M là trung điểm AC.Đường thẳng HM cắt đường thẳng AB tại E. Lấy F sao cho M là trung điểm EF.
a) C/m tứ giác AECF là hbh.
b) Qua F kẻ đường thẳng // với AH, cắt AC tại K. C/m AH/FK = AC/EF.
c) Qua H kẻ đường thẳng // với AB, cắt AF tại Q. Gọi P là giao điểm HC và FK. C/m PQ//AC.
d) Gọi N là trung điểm của AF và D là giao điểm của PQ với FC. C/m 3 điểm K, D, N thẳng hàng