
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=> 25% của 324 là 81
~~~~~~~~~~~~~~~~
=> 25% của 324 = (25/100) x 324 = 0,25 x 324 = 81

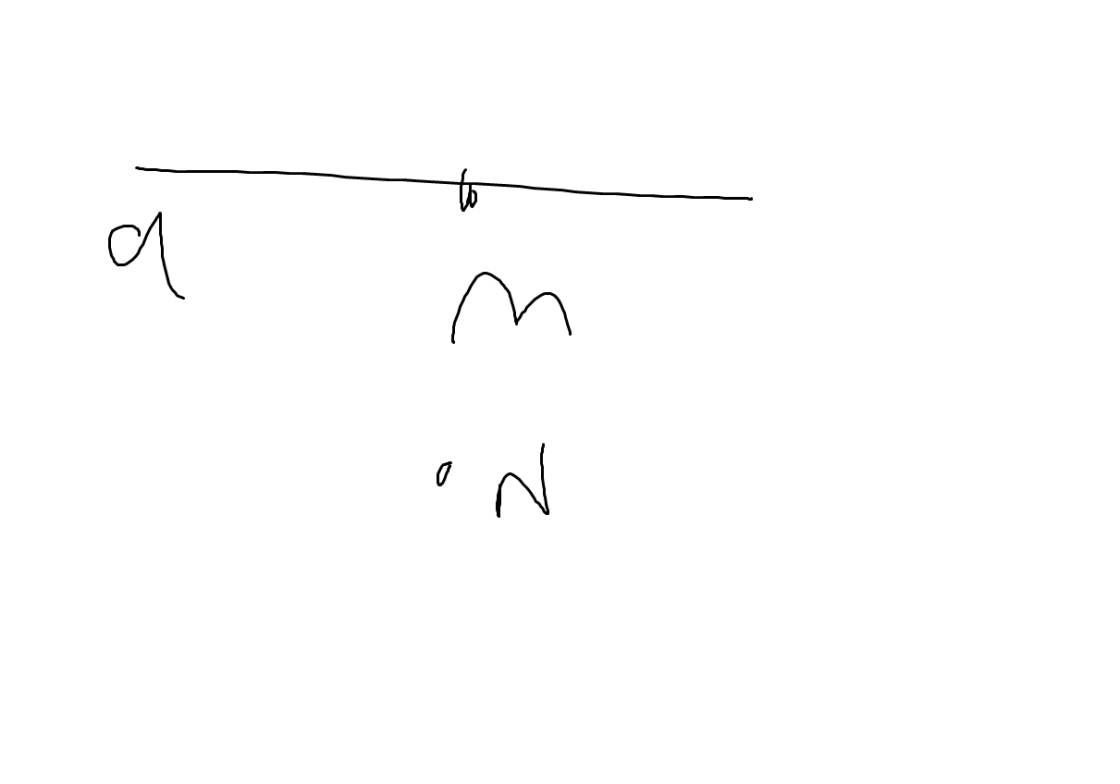
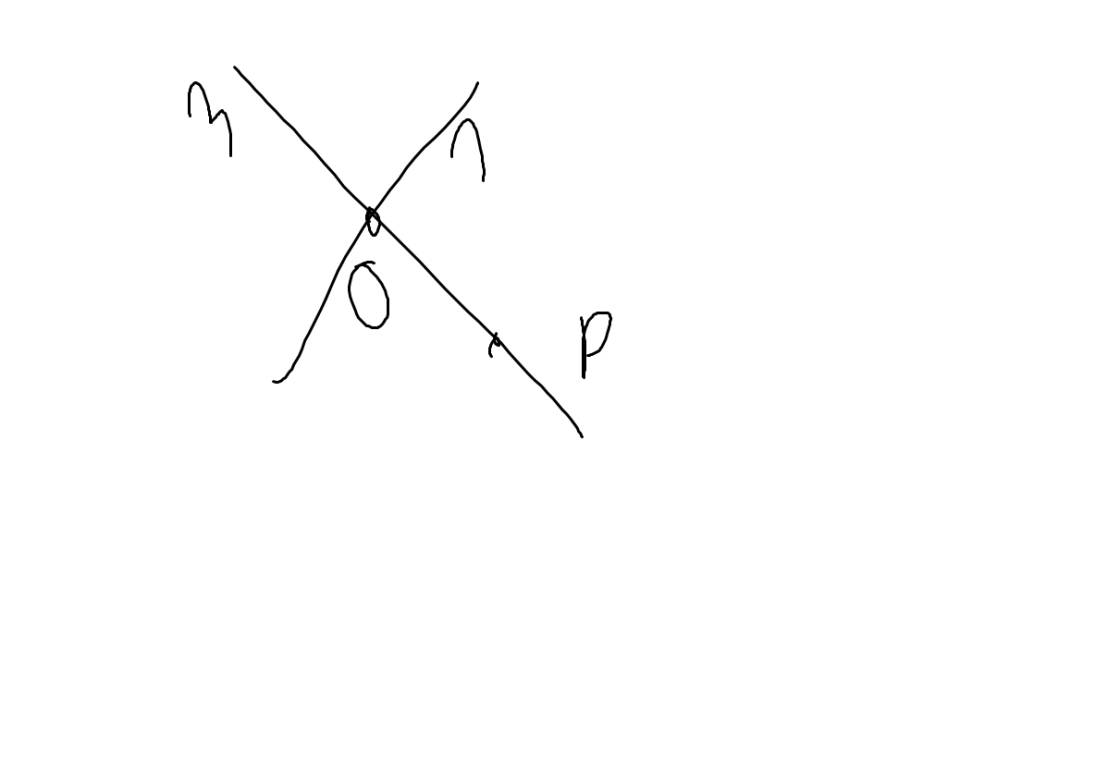
a: Ta có: \(\widehat{BMO}+\widehat{MBO}+\widehat{MOB}=180^0\)
\(\widehat{CON}+\widehat{MON}+\widehat{MOB}=180^0\)
mà \(\widehat{MBO}=\widehat{MON}\left(=60^0\right)\)
nên \(\widehat{BMO}=\widehat{CON}\)
Xét ΔBMO và ΔCON có
\(\widehat{BMO}=\widehat{CON}\)
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMO~ΔCON
b: Ta có: ΔBMO~ΔCON
=>\(\dfrac{OM}{ON}=\dfrac{BM}{CO}\)
mà BO=CO
nên \(\dfrac{OM}{ON}=\dfrac{BM}{BO}\)
c: \(\dfrac{OM}{ON}=\dfrac{BM}{BO}\)
=>\(\dfrac{OM}{BM}=\dfrac{ON}{OB}\)
Xét ΔOMN và ΔBMO có
\(\dfrac{OM}{BM}=\dfrac{ON}{OB}\)
\(\widehat{MON}=\widehat{MBO}=60^0\)
Do đó: ΔMON~ΔMBO
=>\(\widehat{OMN}=\widehat{BMO}\)
=>MO là phân giác của góc BMN

A = 5 + 52 + 53 + ... + 5100
5A = 52 + 53 + 54 + ... + 5101
5A - A = (52 + 53 + 54 + ... + 5101) - (52 + 53 + 54 + ... + 5100)
4A = 52 + 53 + 54 + ... + 5101 - 52 - 53 - 54 - ... - 5100
4A = (52 - 52) + (53 - 53) + (54 - 54) + ... + (5100 - 5100) + (5101 - 5)
4A = 0 + 0 + ... 0 + 5101 - 5
A = \(\dfrac{5^{101}-5}{4}\)
b; 4.A + 5 = 5n
5101 - 5 + 5 = 5n
5101 = 5n
n = 101
Vậy n = 101

a; 54,75 : 1,5 - (\(x+20,4\)) = 3,8
36,5 - (\(x\) + 20,4) = 3,8
\(x\) + 20,4 = 36,5 - 3,8
\(x\) + 20,4 = 32,7
\(x\) = 32,7 - 20,4
\(x\) = 12,3
36,5 - x + 20,4 = 3,8
36,5 - x = 3,8 + 20,4
36,5 - x = 24,2
x = 36,5 -24,2
x = 12,3

Chiều rộng HCN: 10:2=5(cm)
Chu vi HCN: (10+5) x 2 = 30(cm)
Đ,số:...
Chiều rộng hình chữ nhật là :
10 : 2 = 5(cm)
Chu vi hình chữ nhật là
(10+5) x 2 = 30 ( cm)
Chúc em học giỏi nha

Lời giải:
Gọi số tăm tự thiện của cả 3 lớp là $a$.
Với tỉ lệ chia 5/6/7 ban đầu, tổng số phần là $5+6+7=18$.
3 lớp nhận lần lượt $\frac{5a}{18}, \frac{6a}{18}, \frac{7a}{18}$ (gói tăm)
Với tỉ lệ chia 4/5/6 lúc sau, tổng số phần là $4+5+6=15$
3 lớp nhận lần lượt là: $\frac{4a}{15}, \frac{5a}{15}, \frac{6a}{15}$ (gói tăm)
Như vậy, chỉ có lớp 7C là mua nhiều hơn dự định (\frac{6a}{15}>\frac{7a}{18})$
$\Rightarrow \frac{6a}{15}-\frac{7a}{18}=1$
$\Rightarrow \frac{1}{90}a=1$
$\Rightarrow a=90$
a.
Số gói tăm 3 lớp mua là:
7A: $\frac{4a}{15}=\frac{4.90}{15}=24$
7B: $\frac{5a}{15}=30$
7C: $\frac{6a}{15}=36$
b.
Số tiền 3 lớp đã ủng hộ: $90.5000=450000$ (đồng)
Lời giải:
Gọi số tăm tự thiện của cả 3 lớp là $a$.
Với tỉ lệ chia 5/6/7 ban đầu, tổng số phần là $5+6+7=18$.
3 lớp nhận lần lượt $\frac{5a}{18}, \frac{6a}{18}, \frac{7a}{18}$ (gói tăm)
Với tỉ lệ chia 4/5/6 lúc sau, tổng số phần là $4+5+6=15$
3 lớp nhận lần lượt là: $\frac{4a}{15}, \frac{5a}{15}, \frac{6a}{15}$ (gói tăm)
Như vậy, chỉ có lớp 7C là mua nhiều hơn dự định (\frac{6a}{15}>\frac{7a}{18})$
$\Rightarrow \frac{6a}{15}-\frac{7a}{18}=1$
$\Rightarrow \frac{1}{90}a=1$
$\Rightarrow a=90$
a.
Số gói tăm 3 lớp mua là:
7A: $\frac{4a}{15}=\frac{4.90}{15}=24$
7B: $\frac{5a}{15}=30$
7C: $\frac{6a}{15}=36$
b.
Số tiền 3 lớp đã ủng hộ: $90.5000=450000$ (đồng)

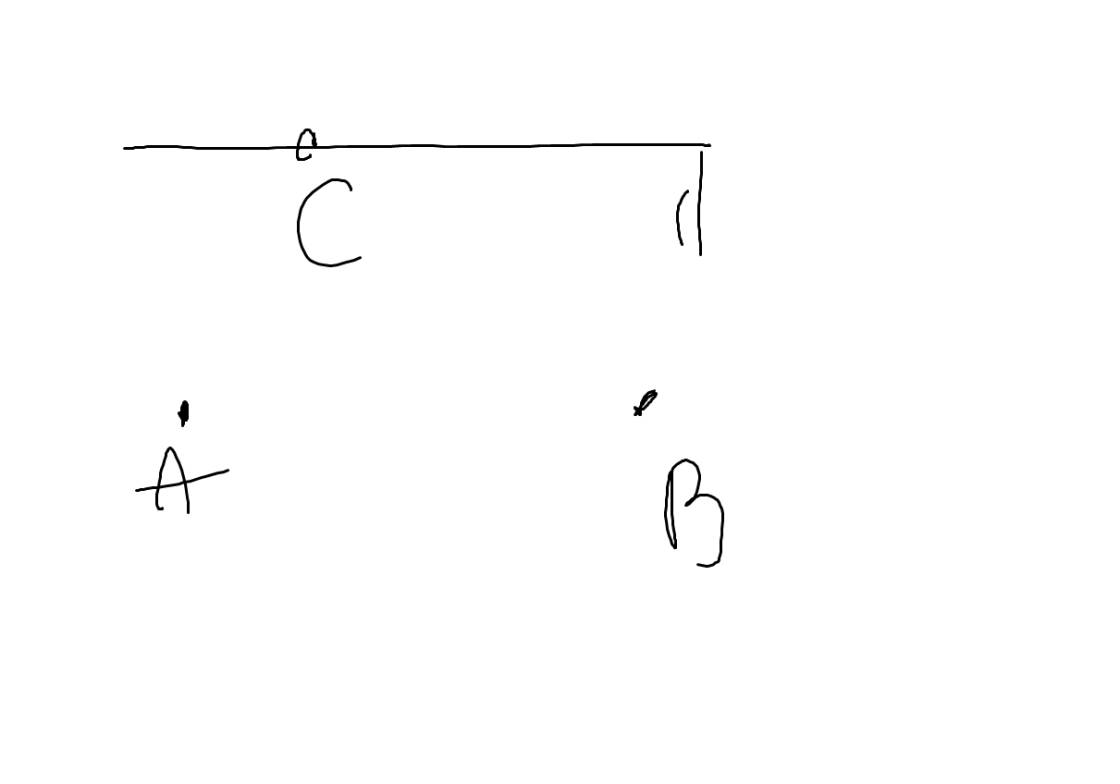
Lời giải:
Đặt $A=\frac{1}{20.23}+\frac{1}{23.26}+\frac{1}{26.29}+...+\frac{1}{77.80}$
$3A=\frac{3}{20.23}+\frac{3}{23.26}+\frac{3}{26.29}+...+\frac{3}{77.80}$
$=\frac{23-20}{20.23}+\frac{26-23}{23.26}+\frac{29-26}{26.29}+...+\frac{80-77}{77.80}$
$=\frac{1}{20}-\frac{1}{23}+\frac{1}{23}-\frac{1}{26}+\frac{1}{26}-\frac{1}{29}+...+\frac{1}{77}-\frac{1}{80}$
$=\frac{1}{20}-\frac{1}{80}$
$A=\frac{1}{3}(\frac{1}{20}-\frac{1}{80})=\frac{1}{60}-\frac{1}{240}< \frac{1}{60}< \frac{1}{9}$
Ta có:
\(\dfrac{1}{20.23}+\dfrac{1}{23.26}+...+\dfrac{1}{77.80}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{20.23}+\dfrac{3}{23.26}+...+\dfrac{3}{77.80}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{20}-\dfrac{1}{23}+\dfrac{1}{23}-\dfrac{1}{26}+...+\dfrac{1}{77}-\dfrac{1}{80}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{20}-\dfrac{1}{80}\right)\)
\(=\dfrac{1}{3}.\dfrac{3}{80}=\dfrac{1}{80}< \dfrac{1}{9}\) (đpcm)