tính giá trị biểu thức
a)\(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}\)
b)\(\dfrac{1}{5}\sqrt{50}-2\sqrt{96}-\dfrac{\sqrt{30}}{\sqrt{15}}+12\sqrt{\dfrac{1}{6}}\)
c)\(\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)
\(A=\left[\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)
\(A=\left[\dfrac{a}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\left[\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right]\)
\(A=\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\left[\dfrac{\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}+\dfrac{2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right]\)
\(A=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(A=\dfrac{\sqrt{a}+1}{\sqrt{a}}:\dfrac{\sqrt{a}+1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(A=\dfrac{\sqrt{a}+1}{\sqrt{a}}\cdot\left(\sqrt{a}-1\right)\)
\(A=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}}\)
\(A=\dfrac{a-1}{\sqrt{a}}\)
b) Ta có:
\(a=4+2\sqrt{3}=\left(\sqrt{3}\right)^2+2\sqrt{3}\cdot1+1^2=\left(\sqrt{3}+1\right)^2\)
Thay vào A ta có:
\(A=\dfrac{\left(\sqrt{3}+1\right)^2-1}{\sqrt{\left(\sqrt{3}+1\right)^2}}=\dfrac{4+2\sqrt{3}-1}{\sqrt{3}+1}=\dfrac{3+2\sqrt{3}}{\sqrt{3}+1}\)
c) \(A< 0\) khi:
\(\dfrac{a-1}{\sqrt{a}}< 0\)
Mà: \(\sqrt{a}\ge0\forall x\) (xác định)
\(\Leftrightarrow a-1< 0\)
\(\Leftrightarrow a< 1\)
Kết hợp với đk:
\(0< a< 1\)

\(\left(x^2-\dfrac{y}{2}\right)^3\)
\(=\left(x^2\right)^3-3\cdot\left(x^2\right)^2\cdot\dfrac{y}{2}+3\cdot x^2\cdot\left(\dfrac{y}{2}\right)^2-\left(\dfrac{y}{2}\right)^3\)
\(=x^6-\dfrac{3x^4y}{2}+\dfrac{3x^2y^2}{4}-\dfrac{y^3}{8}\)

Diện tích 5 cái bánh hình tròn :
\(S_b=5.6.6.3,14.\dfrac{1}{4}=141,3\left(cm^2\right)\)
mà cái hộp đựng 5 cái bánh là hình vuông
Nên cạnh nhỏ nhất của cái hộp là : \(6.3=18\left(cm\right)\)

Để:
1111111*33333333 chia hết cho 7 thì:
⇒ 11111111*3333333 + (3 x 5) phải chia hết cho 7
⇒ 11111111+* x 100000000 + 33333333 + 15 chia hết cho 7
⇒ 44444459 + * x 100000000 chia hết cho 7
⇒ * = 2

\(x^3-6x^2+12x-8\)
\(=x^3-3\cdot2\cdot x^2+3\cdot2^2\cdot x-2^3\)
\(=\left(x-2\right)^3\)
Thay x = 10 ta có:
\(\left(10-2\right)^3=8^3=512\)
\(P=x^3-6x^2+12x-8\)
\(P=x^3-3.x^2.2+3.x.2^2-2^3\)
\(P=\left(x-2\right)^3\)
Tại \(x=10\) thì \(P=\left(10-2\right)^3=512\)
Vậy giá trị của biểu thức đã cho là 512 tại \(x=10\)

Ta có \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)
\(\Leftrightarrow x^2-2xy+y^2+x^2-2xz+z^2+y^2+2yz+z^2\ge0\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2xz-2yz\ge0\)
\(\Leftrightarrow2x^2+2y^2+2z^2\ge2xy+2xz+2yz\)
\(\Leftrightarrow3x^2+3y^2+3z^2\ge x^2+y^2+z^2+2xy+2xz+2yz\)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge3^2\)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge9\)
Áp dụng Bđt Bunhiacopxki cho các cặp số dương \(\left(1;x\right);\left(1;y\right);\left(1;z\right)\)
\(\left(1.x+1.y+1.z\right)^2\le\left(1^2+1^2+1^2\right)\left(x^2+y^2+z^2\right)\)
\(\Leftrightarrow\left(x+y+z\right)^2\le3\left(x^2+y^2+z^2\right)\)
\(\Leftrightarrow P=x^2+y^2+z^2\ge\dfrac{\left(x+y+z\right)^2}{3}=\dfrac{9}{3}=3\)
Dấu "=" xảy ra khi và chỉ khi \(\dfrac{1}{x}=\dfrac{1}{y}=\dfrac{1}{z}\Rightarrow x=y=z=\dfrac{3}{3}=1\)
Vậy \(GTNN\left(P\right)=3\left(tạix=y=z=1\right)\)

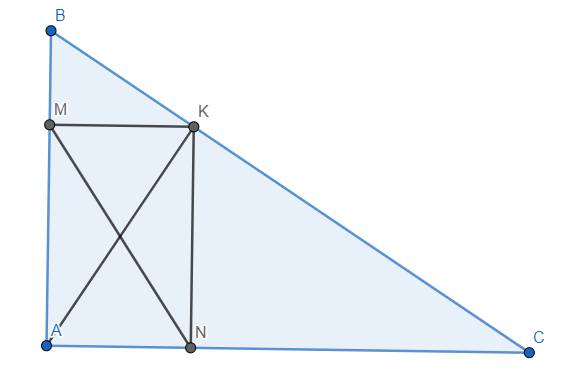
a) Tam giác AKB vuông tại K có đường cao KM nên \(AK^2=AM.AB\)
Chứng minh tương tự, ta có \(AK^2=AN.AC\)
Từ đó suy ra \(AM.AB=AN.AC\) (đpcm)
b) Tam giác KMN vuông tại K nên \(KM^2+KN^2=MN^2\)
Dễ thấy tứ giác AMKN là hình chữ nhật, suy ra \(AK=MN\). Từ đó \(KM^2+KN^2=AK^2\).
Tam giác ABC vuông tại A, đường cao AK nên \(AK^2=KB.KC\)
Thế thì \(KM^2+KN^2=KB.KC\) (đpcm)
c) Tam giác AKB vuông tại K, có đường cao KM nên \(AM.BM=KM^2\)
Tương tự, ta có \(AN.CN=KN^2\)
Từ đó \(AM.BM+AN.CN=KM^2+KN^2\)
Theo câu b), \(KM^2+KN^2=KB.KC\)
Do đó \(AM.BM+AN.CN=KB.KC\) (đpcm)

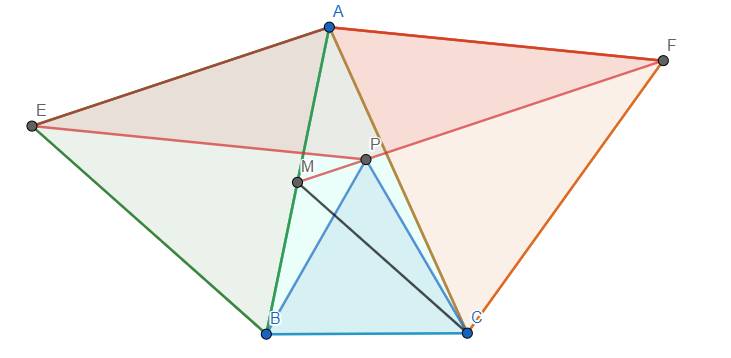
Gọi M là giao điểm của PE với AB.
Ta thấy rằng \(CF=AF=PE,PF=AE=EB\)
Đồng thời \(\widehat{BEP}=60^o-\widehat{AEP}=60^o-\widehat{AFP}=\widehat{PFC}\)
Dẫn đến \(\Delta PBE=\Delta CPF\left(c.g.c\right)\)
\(\Rightarrow PB=PC\) (1)
Mặt khác, \(\widehat{AMF}=\widehat{MAE}=60^o=\widehat{ACF}\) nên tứ giác AMCF nội tiếp.
\(\Rightarrow\widehat{BAC}=\widehat{PFC}\). Mà lại có \(AB=PF,AC=FC\) nên suy ra \(\Delta ABC=\Delta FPC\left(c.g.c\right)\)
\(\Rightarrow PC=BC\) (2)
Từ (1) và (2) \(\Rightarrow\Delta PBC\) đều (đpcm)

\(S=\sqrt[]{1.2007}+\sqrt[]{3.2005}+\sqrt[]{5.2003}+...+\sqrt[]{2007.1}\)
Tổng số hạng của S là :
\(\left(2007-1\right):2+1=1004\left(số,hạng\right)\)
Áp dụng bất đảng Cauchy cho 1004 cặp số \(\left(1;2007\right);\left(3;2005\right);\left(5;2003\right)...\left(2007;1\right)\)
\(\sqrt[]{1.2007}< \dfrac{1+2007}{2}=\dfrac{2008}{2}\)
\(\sqrt[]{3.2005}< \dfrac{3+2005}{2}=\dfrac{2008}{2}\)
\(\sqrt[]{5.2003}< \dfrac{5+2003}{2}=\dfrac{2008}{2}\)
\(.....\)
\(\sqrt[]{2007.1}< \dfrac{2007+1}{2}=\dfrac{2008}{2}\)
\(\Rightarrow S=\sqrt[]{1.2007}+\sqrt[]{3.2005}+\sqrt[]{5.2003}+...+\sqrt[]{2007.1}< 1004.\dfrac{2008}{2}=1004^2\)
Vậy \(S< 1004^2\)

a) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}\)
\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\left(\sqrt{2}-2\right)\)
\(=\left|\sqrt{2}+1\right|-\sqrt{2}+2\)
\(=\sqrt{2}+1-\sqrt{2}+2\)
\(=3\)
b) \(\dfrac{1}{5}\sqrt{50}-2\sqrt{96}-\dfrac{\sqrt{30}}{\sqrt{15}}+12\sqrt{\dfrac{1}{6}}\)
\(=\dfrac{1}{5}\cdot5\sqrt{2}-2\cdot4\sqrt{6}-\sqrt{\dfrac{30}{15}}+\sqrt{\dfrac{144}{6}}\)
\(=\sqrt{2}-8\sqrt{6}-\sqrt{2}+2\sqrt{6}\)
\(=-8\sqrt{6}+2\sqrt{6}\)
\(=-6\sqrt{6}\)
c) \(\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)
\(=\left[\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}}-2\right]\left[\dfrac{4\left(1-\sqrt{5}\right)}{\left(1+\sqrt{5}\right)\left(1-\sqrt{5}\right)}+4\right]\)
\(=\left(\sqrt{5}-1-2\right)\left(\dfrac{4\left(1-\sqrt{5}\right)}{1-5}+4\right)\)
\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}-1+4\right)\)
\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}+3\right)\)
\(=\left(\sqrt{5}\right)^2-3^2\)
\(=-4\)
a) \(\sqrt[]{3+2\sqrt[]{2}}+\sqrt[]{\left(\sqrt[]{2}-2\right)^2}\)
\(=\sqrt[]{2+2\sqrt[]{2}.1+1}+\left|\sqrt[]{2}-2\right|\)
\(=\sqrt[]{\left(\sqrt[]{2}+1\right)^2}+\left(2-\sqrt[]{2}\right)\) \(\left(\left(\sqrt[]{2}\right)^2=2< 2^2=4\right)\)
\(=\left|\sqrt[]{2}+1\right|+2-\sqrt[]{2}\)
\(=\sqrt[]{2}+1+2-\sqrt[]{2}\)
\(=3\)