Rút gọn
3 ( a+b)(a+c)(b+c)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2xy+4xy-5xy=6xy-5xy=xy\)
\(x\left(3+2xy\right)=3x+2x^2y\)

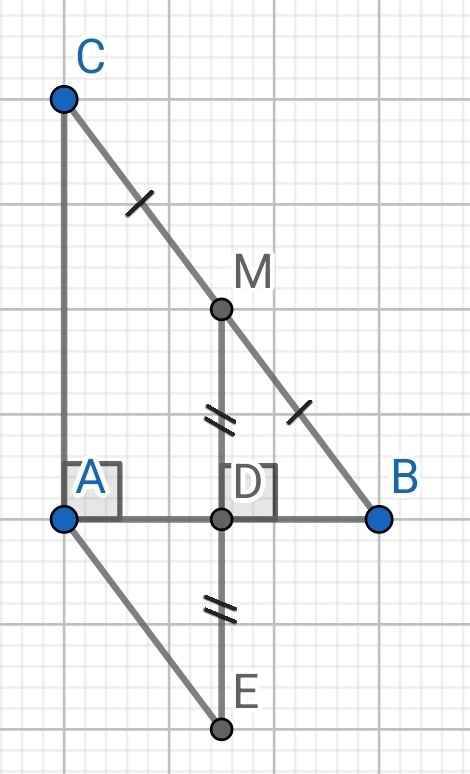 a) Do ∆ABC vuông tại A (gt)
a) Do ∆ABC vuông tại A (gt)
⇒ AB ⊥ AC
Mà MD ⊥ AB (gt)
⇒ AC // MD
⇒ ADMC là hình thang
Mà ∠CAD = 90⁰ (∆ABC vuông tại A)
⇒ ADMC là hình thang vuông
b) ∆ABC có:
M là trung điểm của BC (gt)
MD // AC (cmt)
⇒ D là trung điểm của AB
⇒ MD là đường trung bình của ∆ABC
⇒ MD = AC : 2
⇒ AC = 2MD (1)
Do M và E đối xứng qua D
⇒ D là trung điểm của ME
⇒ ME = 2MD (2)
Từ (1) và (2) ⇒ AC = ME
Do AC // MD (cmt)
⇒ AC // ME
Tứ giác ACME có:
AC // ME (cmt)
AC = ME (cmt)
⇒ ACME là hình bình hành

\(\Leftrightarrow x^2+3xy+3y^2+xy-2x-6y=5\)
\(\Leftrightarrow x\left(x+3y\right)+y\left(x+3y\right)-2\left(x+3y\right)=5\)
\(\Leftrightarrow\left(x+y-2\right)\left(x+3y\right)=5\)
Bảng giá trị:
| x+y-2 | -5 | -1 | 1 | 5 |
| x+3y | -1 | -5 | 5 | 1 |
| x | -4 | 4 | 2 | 10 |
| y | 1 | -3 | 1 | -3 |
Vậy \(\left(x;y\right)=\left(-4;1\right);\left(4;-3\right);\left(2;1\right);\left(10;-3\right)\)

Lời giải:
$2x(y-1)-3(1-y)=2x(y-1)+3(y-1)=(y-1)(2x+3)$
$3x^6-6=3(x^6-2)$

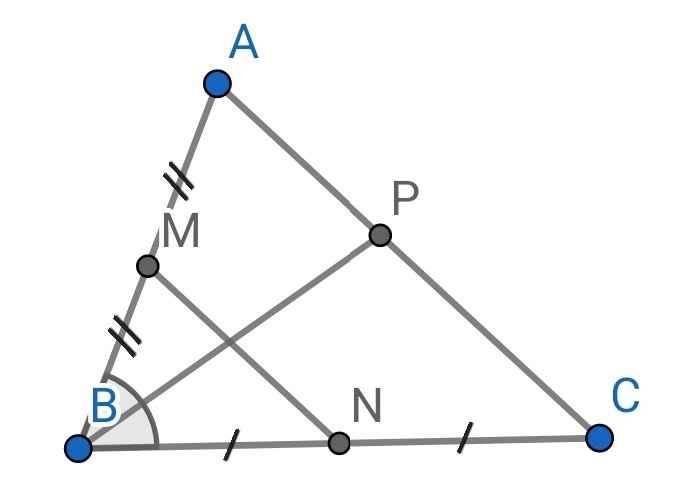 a) Do M là trung điểm của AB (gt)
a) Do M là trung điểm của AB (gt)
⇒ AM = BM = AB : 2 = 6 : 2 = 3 (cm)
Do N là trung điểm của BC (gt)
⇒ BN = CN = BC : 2 = 8 : 2 = 4 (cm)
Ta có:
BM/AM = 3/3 = 1
BN/CN = 4/4 = 1
⇒ BM/AM = BN/CN
⇒ MN // AC (định lý Ta-lét)
b) Ta có:
AM.BC = 3.8 = 24 (cm)
AB.BN = 6.4 = 24 (cm)
⇒ AM.BC = AB.BN
c) Do BP là tia phân giác của ∠ABC (gt)
⇒ BA/BC = PA/PC (1)
Do MN // AC (cmt)
⇒ BA/BC = AM/CN (2)
Từ (1) và (2) ⇒ AM/CN = PA/PC

`#3107.101107`
`3(a + b)(a + c)(b + c)`
`= 3(a^2 + 2ab + bc)(b + c)`
`= 3(a^2b + a^2c + 2ab^2 + 2abc + b^2c + bc^2)`
`= 3a^2b + 3a^2c + 6ab^2 + 6abc + 3b^2c + 3bc^2`