Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(-\dfrac{2}{3}\left(x-\dfrac{1}{4}\right)=\dfrac{1}{3}\left(2x+1\right)\)
=>\(-\dfrac{2}{3}\cdot x+\dfrac{2}{3}\cdot\dfrac{1}{4}=\dfrac{1}{3}\cdot2x+\dfrac{1}{3}\)
=>\(-\dfrac{2}{3}x+\dfrac{2}{12}=\dfrac{2}{3}x+\dfrac{1}{3}\)
=>\(-\dfrac{4}{3}x=\dfrac{1}{3}-\dfrac{2}{12}=\dfrac{1}{6}\)
=>\(x=-\dfrac{1}{6}:\dfrac{4}{3}=-\dfrac{1}{6}\cdot\dfrac{3}{4}=\dfrac{-1}{8}\)
Đặt \(B=\dfrac{1}{2\cdot2}+\dfrac{1}{3\cdot3}+...+\dfrac{1}{10\cdot10}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{10^2}< \dfrac{1}{9}-\dfrac{1}{10}\)
Do đó: \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
=>\(B< 1-\dfrac{1}{10}=\dfrac{9}{10}\)
=>B<1
\(A=2021+\dfrac{1}{2\cdot2}+...+\dfrac{1}{10\cdot10}\)
=>\(A=2021+B< 2021+1=2022\)
Đây là toán nâng cao chuyên đề bịt mắt nhặt bi, cấu trúc thi chuyên, thi học sinh giỏi. Thi violympic, hoomnay olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Trường hợp xấu nhất sẽ bốc phải mỗi màu bút đều có 4 chiếc bút , khi đó tổng số bút bốc được là:
4 + 4 + 4 = 12 (chiếc bút)
Để chắc chắn có 5 chiếc bút cùng màu thì cần bốc ít nhất số lần là:
12 + 1 = 13 (lần)
Đs:...
a: \(\dfrac{18}{31}+\dfrac{11}{31}+\dfrac{12}{31}=\dfrac{18+11+12}{31}=\dfrac{41}{31}\)
b: \(\dfrac{13}{21}+\dfrac{4}{21}+\dfrac{17}{21}=\dfrac{13+4+17}{21}=\dfrac{34}{21}\)
a) $\frac{18}{31} + \frac{11}{31} + \frac{12}{31} = \frac{18+11+12}{31} = \frac{41}{31} = 1\frac{10}{31}$
b) $\frac{13}{21} + \frac{4}{21} + \frac{17}{21} = \frac{13+4+17}{21} = \frac{34}{21} = 1\frac{13}{21}$
Số học sinh chở được trên 1 xe là:
160:4=40(bạn)
Số học sinh tất cả khi có thêm 80 người là:
160+80=240(người)
Số xe cần có là 240:40=6(xe)
Số xe cần bổ sung là 6-4=2(xe)
Bài giải
1 xe chở số học sinh là
160 : 4 = 40 ( học sinh )
Số xe chở 80 học sinh lớp 4 là
80 : 40 = 2 ( xe )
Số xe phải thuê là
4 + 2 = 6 ( xe )
Đáp số 6 xe
$M = a^2 + ab + b^2 - 3a - 3b + 2014$
$M = (a - \frac{3}{2})^2 + (b - \frac{3}{2})^2 + ab + 2014 - \frac{9}{2} - \frac{9}{2}$
$$M = (a - \frac{3}{2})^2 + (b - \frac{3}{2})^2 + ab + 1995$
Vì $(a - \frac{3}{2})^2$ và $(b - \frac{3}{2})^2$ luôn không âm, nên giá trị nhỏ nhất của $M$ sẽ xảy ra khi $(a - \frac{3}{2})^2 = (b - \frac{3}{2})^2 = ab = 0$. Điều này chỉ xảy ra khi $a = b = \frac{3}{2}$.
=> Vậy, giá trị nhỏ nhất của $M$ là $1995$ và xảy ra khi $a = b = \frac{3}{2}$.
a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{MAB}=\widehat{MAC}\)
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔAMB=ΔAMC
=>MB=MC
=>M là trung điểm của BC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Ta có: AM\(\perp\)BC
IH\(\perp\)BC
Do đó: AM//IH
=>\(\widehat{BIH}=\widehat{BAM}\)
mà \(\widehat{BAC}=2\cdot\widehat{BAM}\)(AM là phân giác của góc BAC)
nên \(\widehat{BAC}=2\cdot\widehat{BIH}\)
Giá của 1 quyển truyện là:
49000:7=7000(đồng)
Só tiền Đào có là 28000+49000=77000(đồng)
Số quyển truyện Đào mua được là:
\(\dfrac{77000}{7000}=11\left(quyển\right)\)
Bài giải
Giá của 1 quyển truyện là
49000 : 7 = 7000 ( đồng )
Số truyện Đào mua được là
( 49000 + 28000 ) : 7 = 11 ( quyển )
Đáp số 11 quyển
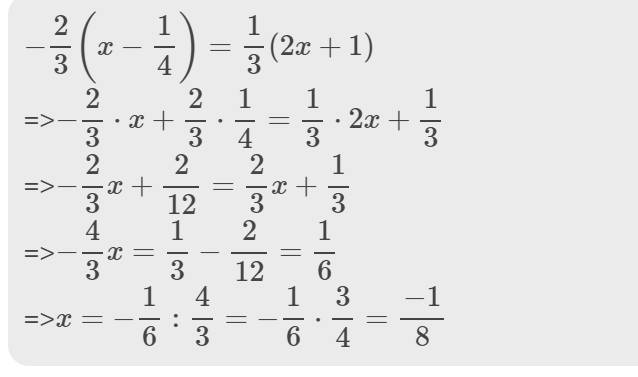
a: D nằm trên đường trung trực của BC
=>DB=DC
=>ΔDBC cân tại D
b: DI là đường trung trực của BC
=>DI\(\perp\)BC tại I
Xét ΔBCD có
CA,DI là các đường cao
CA cắt DI tại H
Do đó: H là trực tâm của ΔBCD
=>BH\(\perp\)CD
c: H nằm trên đường trung trực của BC
=>HB=HC
mà HB>HA(ΔHAB vuông tại A)
nên HC>HA
=>HA<HC