
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Các đường thẳng song song với nhau:
\(y=3-x\) và \(y=-x+2\)
\(y=-4x+2\) và \(y=3-4x\)
Các đường thẳng cắt nhau:
\(y=3-x\) và \(y=-4x+2\)
\(y=3-x\) và \(y=3-4x\)
\(y=-x+2\) và \(y=-4x+2\)
\(y=-x+2\) và \(y=3-4x\)

a.
Hệ số góc \(k=4>0\) nên góc là góc nhọn
b.
Hệ số góc \(k=-\dfrac{3}{4}< 0\) nên góc là góc tù
c.
Hệ số góc \(k=-0,2< 0\) nên góc là góc tù
d.
Hệ số góc \(k=\dfrac{1}{\sqrt{2}}>0\) nên góc là góc nhọn

\(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+c}=1\Rightarrow1-\dfrac{1}{1+a}=\dfrac{1}{1+b}+\dfrac{1}{1+c}\)
\(\Rightarrow\dfrac{a}{1+a}\ge\dfrac{1}{1+b}+\dfrac{1}{1+c}\ge2\sqrt{\dfrac{1}{\left(1+b\right)\left(1+c\right)}}\) (1)
Tương tự ta có:
\(\dfrac{b}{1+b}\ge2\sqrt{\dfrac{1}{\left(1+a\right)\left(1+c\right)}}\) (2)
\(\dfrac{c}{1+c}\ge2\sqrt{\dfrac{1}{\left(1+a\right)\left(1+b\right)}}\) (3)
Nhân vế (1);(2);(3):
\(\Rightarrow\dfrac{abc}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}\ge\dfrac{8}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}\)
\(\Rightarrow abc\ge8\)
Dấu "=" xảy ra khi \(a=b=c=2\)


\(\Leftrightarrow x^4-4x^3+12x^2-32x+32=\left(y-5\right)^2\)
\(\Leftrightarrow\left(x-2\right)^2\left(x^2+8\right)=\left(y-5\right)^2\)
- Với \(x=2\Rightarrow y=5\)
- Với \(x\ne2\Rightarrow x-2\) là ước của \(y-5\)
Đặt \(y-5=n\left(x-2\right)\)
\(\Rightarrow\left(x-2\right)^2\left(x^2+8\right)=n^2\left(x-2\right)^2\)
\(\Rightarrow x^2+8=n^2\)
\(\Rightarrow\left(n-x\right)\left(n+x\right)=8\)
\(\Rightarrow\left[{}\begin{matrix}x=1;n=-3\Rightarrow y=8\\x=-1;n=-3\Rightarrow y=14\\x=1;n=3\Rightarrow y=2\\x=-1;n=3\Rightarrow y=-4\end{matrix}\right.\)

\(\dfrac{x}{x+1}=\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-x}{x^2-1}\)
\(\dfrac{x^2}{1-x}=\dfrac{-x^2}{x-1}=\dfrac{-x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-x^3-x^2}{x^2-1}\)

Gọi số có 4 chữ số thỏa mãn là \(\overline{abcd}\). Khi đó a có 4 cách chọn (từ 1 đến 4). Còn các chữ số b, c, d đều có 5 cách chọn (từ 0 đến 4). Do đó có tất cả \(4.5.5.5=500\) số thỏa mãn ycbt.

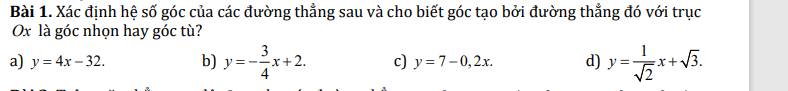

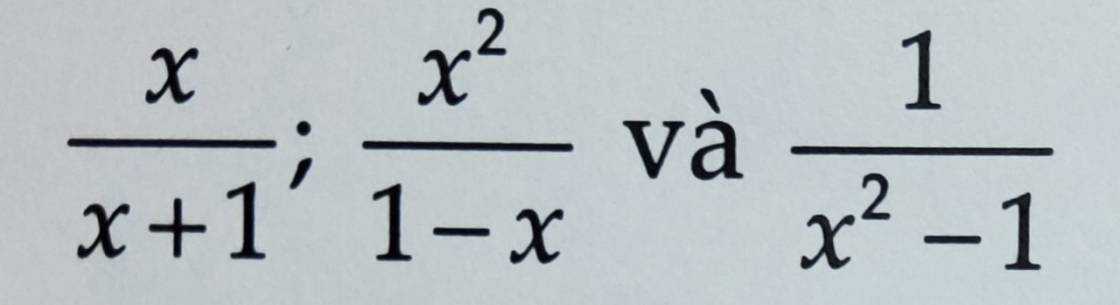
Lời giải:
a. Vì $y=ax+b$ song song với $y=2x+3$ nên $a=2$
b.
Gọi $\alpha$ là góc tạo bởi $y=ax+b$ và trục hoành
Có: $\tan \alpha = a=2$
$\Rightarrow \alpha = 63,43^0$
$\Rightarrow \alpha$ là góc nhọn.
c.
Đường thẳng cắt trục tung tại điểm có tung độ 5, tức là đi qua điểm $(0;5)$
$\Rightarrow 5=a.0+b\Rightarrow b=5$