một hình thoi có tổng độ dài hai đường chéo là 411 m , đường chéo thứ nhất gấp đôi đường chéo thứ hai .tính diện tích hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)
=5145484985742651291274572147214912742724765142721567
\(\text{Viết các số 9673,3547:}\)\(\overline{abcde}\)\(\text{ dưới dạng tổng các luỹ thừa của 10.}\)

`9673=9000+600+70+3`
`=9*10^3+6*10^2+7*10+3`
`3547=3000+500+40+7`
`=3*10^3+5*10^2+4*10+7`
\(\overline{abcde}\)`=a*10000+b*1000+c*100+d*10+e`
`=a*10^4+b*10^3+c*10^2+d*10+e`
\(9673=9\cdot10^3+6\cdot10^2+7\cdot10^1+3\cdot10^0\\ 3547=3\cdot10^3+5\cdot10^2+4\cdot10^1+7\cdot10^0\\ abcde=a\cdot10^4+b\cdot10^3+c\cdot10^2+d\cdot10^1+e\cdot10^0\)

\(\dfrac{2}{5\times7}+\dfrac{2}{7\times9}+...+\dfrac{2}{13\times15}\)
\(=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{13}-\dfrac{1}{15}\)
\(=\dfrac{1}{5}-\dfrac{1}{15}=\dfrac{2}{15}\)
`2/(5 xx 7)+2/(7 xx 9) + ... + 2/(13 xx 15)`
`=1/5-1/7+1/7-1/9+...+1/13-1/15`
`=1/5+(1/7-1/7)+(1/9-1/9)+...+(1/13-1/13)-1/15`
`=1/5-1/15`
`=3/15-1/15`
`=2/15`

Ta có:
\(25^9=\left(5^2\right)^9=5^{18}\)
Vì: \(5^{17}< 5^{18}\) nên \(5^{17}< 25^9\)
Ta có:
\(3^{90}=\left(3^3\right)^{30}=27^{30}\)
\(4^{60}=\left(4^2\right)^{30}=16^{30}\)
Vì: \(27^{30}>16^{30}\) nên \(3^{90}>4^{60}\)
Bài 1:
c: \(18\cdot\left[\left(3^4\cdot29+3^4\cdot6+3^4\cdot34\right)-71\cdot1^{56}\right]-80\)
\(=18\cdot\left[3^4\left(29+6+34\right)-71\right]-80\)
\(=18\cdot\left[81\cdot69-71\right]-80\)
\(=18\cdot5518-80=99244\)
b: \(\left[19+\left(3^5-62\right)\right]\cdot x=10^3\cdot10\)
=>\(\left(243-62+19\right)\cdot x=10000\)
=>\(200x=10000\)
=>x=10000:200=50
Bài 2:
\(25^9=\left(5^2\right)^9=5^{18}>5^{17}\)
\(3^{90}=\left(3^3\right)^{30}=27^{30};4^{60}=\left(4^2\right)^{30}=16^{30}\)
mà 27>16
nên \(3^{90}>4^{60}\)

Chiều cao của hình bình hành là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là \(47\cdot\dfrac{27}{2}=634,5\left(m^2\right)\)
Sau khi mở rộng, cạnh đáy mới là:
\(47+7=54\left(m\right)\)
Chiều cao hình bình hành sau khi tăng là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là:
\(47\cdot27=1269\left(m^2\right)\)
Đáp số: \(1269m^2\)

a: \(\left|x+\dfrac{1}{2}\right|>=0\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)
=>\(x=-\dfrac{1}{2}\)
b: \(\left|x-\dfrac{1}{3}\right|>=0\forall x\)
=>\(\left|x-\dfrac{1}{3}\right|+2>=2\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{3}=0\)
=>\(x=\dfrac{1}{3}\)

\(\left(x-2\right)^2-\left(x+1\right)\left(x-3\right)=-7\\ \Rightarrow x^2-4x+4-\left(x^2-2x-3\right)=-7\\ \Rightarrow x^2-4x+4-x^2+2x+3=-7\\ \Rightarrow-2x+7=-7\\ \Rightarrow-2x=-14\\ \Rightarrow x=-14:\left(-2\right)\\ \Rightarrow x=7\)

Ta có:
`x^2+4x+1`
`=(x^2+4x+4)-3`
`=(x+2)^2-3`
`(x+2)^2>=0` với mọi x
`=>(x+2)^2-3>=-3` với mọi x
Dấu "=" xảy ra:
`x+2=0<=>x=2`
Vậy: ...
Ta có:
\(x^2+4x+1\\ =x^2+4x+2-1\\ =\left(x+2\right)^2-1\)
Vì: \(\left(x+2\right)^2\ge0\rightarrow\left(x+2\right)^2-1\ge-1\forall x\)
Vậy: GTNN là: \(-1\)
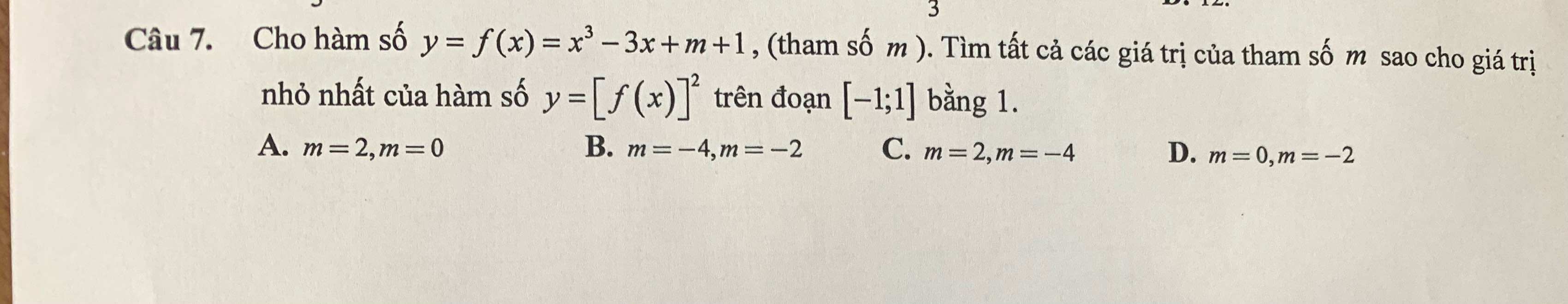

Độ dài đường chéo thứ nhất là:
411:3x2=274(m)
Độ dài đường chéo thứ hai là:
274:2=137(m)
Diện tích hình thoi là: \(274\cdot\dfrac{137}{2}=18769\left(m^2\right)\)
Tỉ số đường chéo thứ nhất và đường chéo thứ hai là: \(\dfrac{2}{1}\)
Tổng số phần bằng nhau là:
\(2+1=3\) (phần)
Đường chéo thứ nhất là:
\(411:3\cdot2=274\left(m\right)\)
Đường chéo thứ hai là:
\(411-274=137\left(m\right)\)
Diện tích hình thoi là:
\(\dfrac{274\cdot137}{2}=18769\left(m^2\right)\)
Đáp số: \(18769m^2\)