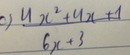banj vieets laij deef ddi

\(\frac{1-4x^2}{x^2+4x}\div\frac{2-4x}{3x}\)

ĐKXĐ : \(\hept{\begin{cases}x\ne0\\x\ne-4\\x\ne\frac{1}{2}\end{cases}}\)

\(=\frac{\left(1-2x\right)\left(1+2x\right)}{x\left(x+4\right)}\times\frac{3x}{2\left(1-2x\right)}\)

\(=\frac{3x\left(1+2x\right)}{2x\left(x+4\right)}\)

\(=\frac{3\left(1+2x\right)}{2\left(x+4\right)}=\frac{6x+3}{2x+8}\)

\(x\left(x+4\right)\left(x+6\right)\left(x+10\right)+128\)

\(=\left(x^2+4x\right)\left(x^2+16x+60\right)+128\)

\(=x^4+16x^3+60x^2+4x^3+64x^2+240x+128\)

\(=x^4+20x^3+124x^2+240x+128\)

x( x + 4 )( x + 6 )( x + 10 ) + 128

= [ x( x + 10 ) ][ ( x + 4 )( x + 6 ) ] + 128

= ( x² + 10x )( x² + 10x + 24 ) + 128

Đặt t = x² + 10x

= t( t + 24 ) + 128

= t² + 24t + 128

= t² + 8t + 16t + 128

= t( t + 8 ) + 16( t + 8 )

= ( t + 8 )( t + 16 )

= ( x² + 10x + 8 )( x² + 10x + 16 )

= ( x² + 10x + 8 )( x² + 2x + 8x + 16 )

= ( x² + 10x + 8 )[ x( x + 2 ) + 8( x + 2 ) ]

= ( x² + 10x + 8 )( x + 2 )( x + 8 )

nếu bn đưa = bao nhiêu mới giải đc

Bài 1 : 

a, sai đề 

b, \(\frac{x^2-xy-x+y}{x^2+xy-x-y}=\frac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\frac{\left(x-1\right)\left(x-y\right)}{\left(x-1\right)\left(x+y\right)}=\frac{x-y}{x+y}\)

Bài 2 : 

a, \(\frac{3x-7x}{3x-5x}-\frac{4x-7}{3x-5}=2-\frac{4x-7}{3x-5}=\frac{2\left(3x-5\right)-4x-7}{3x-5}\)

\(=\frac{6x-10-4x-7}{3x-5}=\frac{2x-17}{3x-5}\)

b, \(\frac{x^3-1}{x^3+x^2+x}-\frac{x^2-4}{6y-3xy}=\frac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x^2+x+1\right)}-\frac{\left(x-2\right)\left(x+2\right)}{3y\left(2-x\right)}\)

\(=\frac{x-1}{x}-\frac{-\left(2-x\right)\left(x+2\right)}{3y\left(2-x\right)}=\frac{x-1}{x}+\frac{x+2}{3y}\)

Bài làm 

\(\frac{4x^2+4x+1}{6x+3}=\frac{\left(2x+1\right)^2}{3\left(2x+1\right)}=\frac{2x+1}{3}\)

Học tốt 

Ta có: \(ax+by+cz=0\)

\(\Rightarrow\left(ax+by+cz\right)^2=0\)

\(\Rightarrow a^2x^2+b^2y^2+c^2z^2+2\left(axby+bycz+axcz\right)=0\)

\(\Rightarrow a^2x^2+b^2y^2+c^2z^2=-2\left(axby+bycz+axcz\right)\)

Lại có: \(\frac{ax^2+by^2+cz^2}{bc\left(y-z\right)^2+ac\left(x-z\right)^2+ab\left(x-y\right)^2}\)

\(=\frac{ax^2+by^2+cz^2}{bc\left(y^2-2yz+z^2\right)+ac\left(x^2-2xz+z^2\right)+ab\left(x^2-2xy+y^2\right)}\)

\(=\frac{ax^2+by^2+cz^2}{bcy^2-2bcyz+bcz^2+acx^2-2acxz+acz^2+abx^2-2abxy+aby^2}\)

\(=\frac{ax^2+by^2+cz^2}{bcy^2+bcz^2+acx^2+acz^2+abx^2+aby^2-2\left(bcyz+acxz+abxy\right)}\)

\(=\frac{ax^2+by^2+cz^2}{bcy^2+bcz^2+acx^2+acz^2+abx^2+aby^2+a^2x^2+b^2y^2+c^2z^2}\)

\(=\frac{ax^2+by^2+cz^2}{\left(acx^2+abx^2+a^2x^2\right)+\left(bcy^2+aby^2+b^2y^2\right)+\left(bcz^2+acz^2+c^2z^2\right)}\)

\(=\frac{ax^2+by^2+cz^2}{ax^2\left(c+b+a\right)+by^2\left(c+a+b\right)+cz^2\left(b+a+c\right)}\)

\(=\frac{ax^2+by^2+cz^2}{\left(a+b+c\right)\left(ax^2+by^2+cz^2\right)}=\frac{1}{a+b+c}=\frac{1}{\frac{1}{2020}}=2020\)  (đpcm)