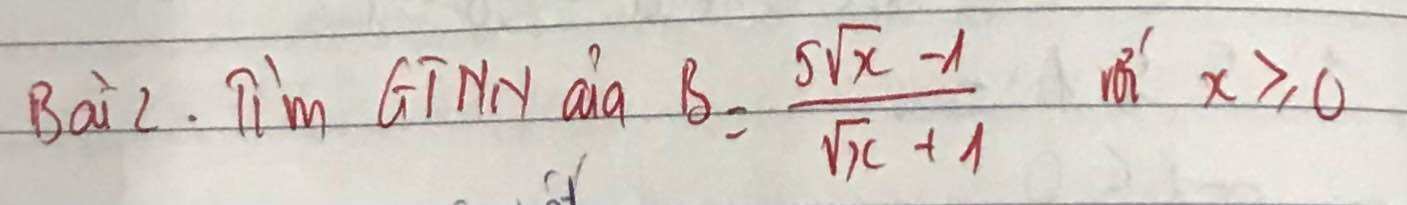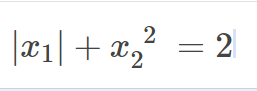a: Khối lượng đường dùng cho x bánh dẻo là 100x(gam)

Khối lượng bột mỳ dùng cho x bánh dẻo là 250x(gam)

Khối lượng đường dùng cho y bánh nướng là 80y(gam)

Khối lượng bột mỳ dùng cho y bánh dẻo là 200y(gam)

Người ta đã dùng 11,4kg đường=11400 gam đường và 28,5kg bột mỳ=28500gam bột mỳ nên ta có:

\(\left\{{}\begin{matrix}100x+80y=11400\\250x+200y=28500\end{matrix}\right.\)

b: Thay x=50;y=80 vào hệ, ta được:

\(\left\{{}\begin{matrix}100\cdot50+80\cdot80=11400\\250\cdot50+200\cdot80=28500\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5000+6400=11400\\12500+16000=28500\end{matrix}\right.\)(đúng)

Vậy: (50;80) là nghiệm của hệ

Xem lại đề x + 3 hay x + 2 

Giá tiền phải trả khi mua xoài là: 

`25000x` (đồng)

Giá tiền phải trả khi mua nhãn là:

`20000y` (đồng)

Mà tổng số tiền phải trả là 200000 đồng nên ta có pt:

`25000x+20000y=200000`

`<=>25x+20y=200`

`<=>5x+4y=40`

2 Nghiệm của pt là: (4;5); (0;10) 

ĐK: `x>=0` 

Ta có:

\(B=\dfrac{5\sqrt{x}-1}{\sqrt{x}+1}\\ =\dfrac{\left(5\sqrt{x}+5\right)-6}{\sqrt{x}+1}=\dfrac{5\left(\sqrt{x}+1\right)-6}{\sqrt{x}+1}\\ =\dfrac{5\left(\sqrt{x}+1\right)}{\sqrt{x}+1}-\dfrac{6}{\sqrt{x}+1}\\ =5-\dfrac{6}{\sqrt{x}+1}\)

Vì: \(\sqrt{x}\ge0\forall x\)

\(=>\sqrt{x}+1\ge1\forall x=>\dfrac{6}{\sqrt{x}+1}\le6\\ =>5-\dfrac{6}{\sqrt{x}+1}\ge5-6=-1\)

Dấu "=" xảy ra: `x=0` 

Ta có pt hoành độ giao điểm là: 

\(-x^2=\left(2-m\right)x+m-3\\ \Leftrightarrow x^2+\left(2-m\right)x+m-3=0\)

Để pt có nghiệm phân biệt thì: 

\(\Delta=\left(2-m\right)^2-4\cdot1\cdot\left(m-3\right)\\ =4-4m+m^2-4m+12=m^2-8m+16=\left(m-4\right)^2>0\) 

`=>m-4<>0<=>m<>4` 

Ta có: `a+b+c=1+(2-m)+(m-3)=0`

\(=>x_1=1\)
Theo vi-ét ta có: \(x_1+x_2=m-2=>x_2=m-2-x_2=m-2-1=m-3\) 

\(\left|x_1\right|+x_2^2=2\\ =>1+\left(m-3\right)^2=2\\< =>\left(m-3\right)^2=2-1=1\\ < =>\left[{}\begin{matrix}m-3=1\\m-3=-1\end{matrix}\right.\\ < =>\left[{}\begin{matrix}m=1+3=4\left(ktm\right)\\m=-1+3=2\left(tm\right)\end{matrix}\right.\)

Vậy: ... 

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(HB=\sqrt{15^2-9^2}=12\left(cm\right)\)

ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

=>\(BC=2\cdot BH=24\left(cm\right)\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{15^2+15^2-24^2}{2\cdot15\cdot15}=\dfrac{-7}{25}\)

=>\(sinBAC=\sqrt{1-\left(-\dfrac{7}{25}\right)^2}=\sqrt{1-\dfrac{49}{625}}=\dfrac{24}{25}\)

Xét ΔABC có \(\dfrac{BC}{sinBAC}=2R\)

=>\(2R=24:\dfrac{24}{25}=25\)

=>R=12,5(cm)

A = (\(\dfrac{1}{x-\sqrt{x}}\)  + \(\dfrac{1}{\sqrt{x}+1}\)) : \(\sqrt{x}\) + \(\dfrac{1}{x-2\sqrt{x}+1}\)

Có phải đề bài như này không em?

Để chứng minh rằng (2 + \frac{3}{2} + \frac{5}{2}) là số vô tỉ, ta cần chứng minh rằng tổng này không thể biểu diễn dưới dạng một tỉ số của hai số nguyên. Để làm điều này, ta có thể chứng minh bằng phản chứng, giả sử rằng tổng đó là một số tỉ.

nhớ tick cho mik nhé