Tham khảo
Ta có AB<BC<AC mà điểm B nằm trên đường thẳng AC do đó B nằm giữa A và C

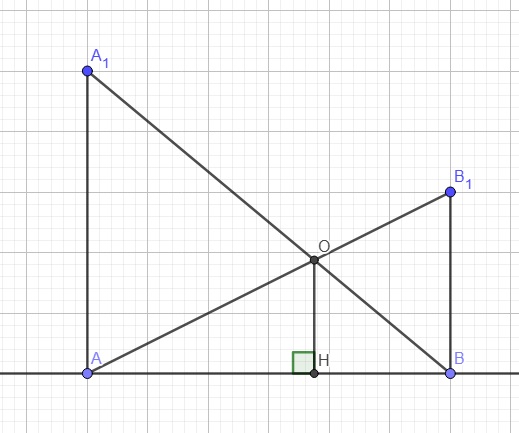
Gọi H là hình chiếu vuông góc của O lên d

\(\Rightarrow AA_1||OH||BB_1\)

Áp dụng định lý Thales trong tam giác \(ABA_1\)

\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)

Áp dụng định lý Thales trong tam giác \(ABB_1\)

\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)

\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)

\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)

\(\Rightarrow OH=\dfrac{a.b}{a+b}\)

Do a, b không đổi \(\Rightarrow OH\) không đổi

Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d

Giải:

(\(x-3\))\(^5\) = 4.(\(x-3\))\(^3\)

(\(x-3\))\(^5\) - 4.(\(x-3\))\(^3\) = 0

(\(x-3\))\(^3\).[(\(x-3)^2\) - 4] = 0

\(\left[\begin{array}{l}x-3=0\\ \left(x-3\right)^2=4\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x-3=-2\\ x-3=2\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x=-2+3\\ x=2+3\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x=1\\ x=5\end{array}\right.\)

Vậy \(x\in\left\lbrace1;3;5\right\rbrace\)

(x - 3)⁵ = 4(x - 3)³

(x - 3)⁵ - 4(x - 3)³ = 0

(x - 3)³.[(x - 3)² - 4] = 0

(x - 3)³.(x - 3 - 2)(x - 3 + 2) = 0

(x - 3)³(x - 5)(x - 1) = 0

(x - 3)³ = 0 hoặc x - 5 = 0 hoặc x - 1 = 0

*) (x - 3)³ = 0

x - 3 = 0

x = 3

*) x - 5 = 0

x = 5

*) x - 1 = 0

x = 1

Vậy x = 1; x = 3; x = 5

bằng 6708

a: Bảng tần số:

Tần số tương ứng của giá trị 32 là \(\dfrac{6}{20}=30\%\)

=>Sai

b: Sai

c: Sai

d: Sai

\(a=\frac72\) ​,b=3

f(2)=0

=>\(2^2+a\cdot2+b=0\)

=>2a+b=-4

=>b=-4-2a

=>\(f\left(x\right)=x^2+ax-2a-4\)

f(x) chia hết cho 2x-3

=>\(x^2+ax-2a-4⋮2x-3\)

=>\(x^2-1,5x+\left(a+1,5\right)x-\left(1,5a+2,25\right)+1,5a+2,25-2a-4⋮2x-3\)

=>-0,5a-1,75=0

=>0,5a=-1,75

=>a=-3,5

b=-4-2a=-4+7=3

a: \(CN=\dfrac{1}{3}CB\)

=>\(S_{ANC}=\dfrac{1}{3}\times S_{ABC}=\dfrac{180}{3}=60\left(cm^2\right)\)

\(CM=\dfrac{1}{2}CA\)

=>\(S_{CMN}=\dfrac{1}{2}\times S_{ANC}=30\left(cm^2\right)\)

Ta có: \(S_{CMN}+S_{AMNB}=S_{ACB}\)

=>\(S_{AMNB}=180-30=150\left(cm^2\right)\)