1/3×5 + 1/5×7 + 1/7×9+...+ 1/25×27
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giá tiền vốn của 20 xe đạp là:
\(1600000:8\%=20000000\left(đ\right)\)
Cửa hàng bán 1 xe đạp giá:
\(20000000:20=2000000\left(đ\right)\)
Đáp số: 2 000 000 đồng

a: \(CN=\dfrac{2}{3}CA\)
=>\(S_{BNC}=\dfrac{2}{3}\times S_{ABC}=\dfrac{2}{3}\times216=144\left(cm^2\right)\)
=>\(S_{ABN}=216-144=72\left(cm^2\right)\)
Vì BM=2/3BA
nên \(AM=\dfrac{1}{3}AB\)
=>\(S_{AMN}=\dfrac{1}{3}\times S_{ABN}=24\left(cm^2\right)\)
b: Vì BI=2/3BC
nên \(CI=\dfrac{1}{3}CB\)
=>\(S_{CIN}=\dfrac{1}{3}\times S_{NBC}=\dfrac{1}{3}\times144=48\left(cm^2\right)\)
\(S_{AMN}+S_{BMNI}+S_{NIC}=S_{ABC}\)
=>\(S_{BMNI}+48+24=216\)
=>\(S_{BMNI}=144\left(cm^2\right)\)

khi ta chuyển dấu phảy của số đó sang trái hai chữ số thì số đó sẽ giảm đi 100 lần. Vậy, t có sơ đồ:
số cũ: 100 phần
số mới: 1 phần
hiệu: 200,376
số cần tìm là: 200,376: (100-1)x 100= 202,4
đáp số: 202,4
khi ta chuyển dấu phảy của số đó sang trái hai chữ số thì số đó sẽ giảm đi 100 lần. Vậy, t có sơ đồ:
số cũ: 100 phần
số mới: 1 phần
hiệu: 200,376
số cần tìm là: 200,376: (100-1)x 100= 202,4
đáp số: 202,4

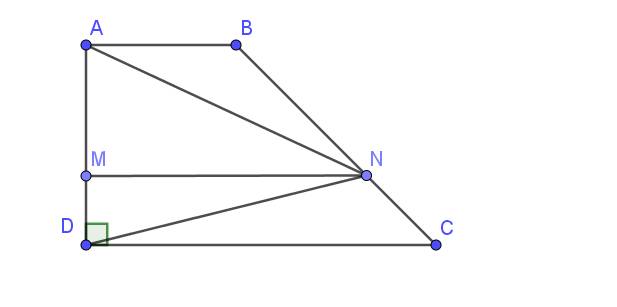
Lời giải:
$S_{ABCD}=(AB+CD)\times AD:2=(20+40)\times 25:2=750$ (m2)
$S_{ABN}=AM\times AB:2=(AD-MD)\times AB:2=(25-8)\times 20:2=170$ (m2)
$S_{CDN}=CD\times MD:2=40\times 8:2=160$ (m2)
$S_{ADN}=MN\times AD:2=S_{ABCD}-S_{ABN}-S_{CDN}$
$MN\times 25:2=750-170-160$
$MN\times 25:2=420$
$MN=420\times 2:25=33,6$ (m)
$S_{ABNM}=(AB+MN)\times AM:2=(20+33,6)\times (25-8):2=455,6$ (m2)

(Bạn tự vẽ hình nhé)
Nối AM
\(\dfrac{S.MNC}{S.AMC}\)=\(\dfrac{NC}{AC}\)=\(\dfrac{2}{3}\) (Chung chiều cao hạ từ M -> AC)
=> S.AMC = 8 : 2 x 3 = 12 (cm2)
\(\dfrac{S.AMC}{S.ABC}\)=\(\dfrac{MC}{BC}\)=\(\dfrac{3}{4}\) (Chung chiều cao hạ từ A -> BC)
=> S.ABC = 12 : 3 x 4 = 16 (cm2)
Đáp số: 16 cm2
Học tốt!!!

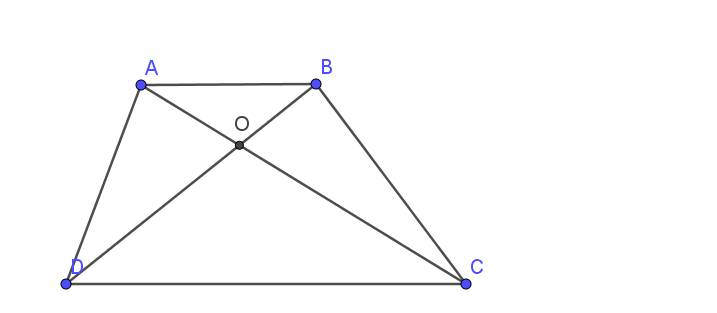
Lời giải:
a. Tổng độ dài hai đáy:
$48\times 2:6=16$ (cm)
Độ dài đáy nhỏ: $(16-4):2=6$ (cm)
Độ dài đáy lớn: $6+4=10$ (cm)
b.
$S_{ABD}=AB\times h:2=6\times 6:2=18$ (cm2)
$S_{ABC}=AB\times h:2 = 6\times 6:2=18$ (cm2)
$\Rightarrow S_{ABD}=S_{ABC}$
$\Rightarrow S_{ABD}-S_{AOB}=S_{ABC}-S_{AOB}$
$\Rightarrow S_{AOD}=S_{BOC}$
d.
$\frac{S_{AOB}}{S_{AOD}}=\frac{OB}{OD}$
$\Rightarrow S_{AOB}=\frac{OB}{OD}\times S_{AOD}$
$\frac{S_{BOC}}{S_{DOC}}=\frac{OB}{OD}$
$\Rightarrow S_{BOC}=\frac{OB}{OD}\times S_{DOC}$
Suy ra:
$S_{AOB}+S_{BOC}=\frac{OB}{OD}\times (S_{AOD}+S_{DOC})$
$S_{ABC}=\frac{OB}{OD}\times S_{ADC}$
$6\times 6:2=\frac{OB}{OD}\times 10\times 6:2$
$18=\frac{OB}{OD}\times 30$
$\frac{OB}{OD}=\frac{18}{30}=\frac{3}{5}$
$\Rightarrow \frac{OB}{BD}=\frac{3}{8}$
$\frac{S_{AOB}}{S_{ABD}}=\frac{OB}{BD}=\frac{3}{8}$
$\Rightarrow S_{AOB}=\frac{3}{8}\times S_{ABD}=\frac{3}{8}\times 18=6,75$ (cm2)


\(3-\left(\dfrac{1}{6}+x\right)\cdot\dfrac{2}{3}=\dfrac{2}{3}\\ \left(\dfrac{1}{6}+x\right)\cdot\dfrac{2}{3}=\dfrac{7}{3}\\ \dfrac{1}{6}+x=\dfrac{7}{2}\\ x=\dfrac{7}{2}-\dfrac{1}{6}=\dfrac{10}{3}\)
HD:
\(\dfrac{2}{3}\) x\(\left(\dfrac{1}{6}+x\right)=3-\dfrac{2}{3}\)
\(\left(\dfrac{1}{6}+x\right)=\dfrac{7}{3}:\dfrac{2}{3}\)
\(x=\dfrac{7}{2}-\dfrac{1}{6}\)
\(x=\dfrac{10}{3}\)
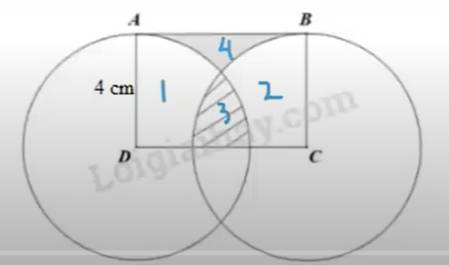 Ngày mai thi NNT rồi, mik đg ôn mà ko bt bài này bạn nào có thể giải chi tiết và lý do tại sao bạn lại làm như vậy được không ?
Ngày mai thi NNT rồi, mik đg ôn mà ko bt bài này bạn nào có thể giải chi tiết và lý do tại sao bạn lại làm như vậy được không ?

\(\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+...+\dfrac{1}{25\times27}\)
\(=\dfrac{1}{2}\times\left(\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+...+\dfrac{1}{25\times27}\right)\)
\(=\dfrac{1}{2}\times\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{25}-\dfrac{1}{27}\right)\)
\(=\dfrac{1}{2}\times\left(\dfrac{1}{3}-\dfrac{1}{27}\right)\)
\(=\dfrac{1}{2}\times\dfrac{8}{27}\)
\(=1\times\dfrac{4}{27}=\dfrac{4}{27}\)
\(\dfrac{1}{3\text{x}5}+\dfrac{1}{5\text{x}7}+...+\dfrac{1}{25\text{x}27}\)
\(=\dfrac{1}{2}\text{x}\left(\dfrac{2}{3\text{x}5}+\dfrac{2}{5\text{x}7}+...+\dfrac{2}{25\text{x}27}\right)\)
\(=\dfrac{1}{2}\text{x}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{25}-\dfrac{1}{27}\right)\)
\(=\dfrac{1}{2}\text{x}\left(\dfrac{1}{3}-\dfrac{1}{27}\right)=\dfrac{1}{2}\text{x}\dfrac{8}{27}=\dfrac{4}{27}\)