Tính \(B=\frac{3x-2y}{3x+2y}\)biết \(9x^2+4y^2=20xy\)và \(2y.3x< 0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : x2 - 2y2 = xy
=> x2 - xy - 2y2 = 0
=> x2 + xy - 2xy - 2y2 = 0
=> x(x + y) - 2y(x + y) = 0
=> (x - 2y)(x + y) = 0
=> \(\orbr{\begin{cases}x-2y=0\\x+y=0\left(\text{loại}\right)\end{cases}\Rightarrow x=2y}\)
Thay x = 2y vào A ta có
\(A=\frac{x-y}{x+y}=\frac{2y-y}{2y+y}=\frac{y}{3y}=\frac{1}{3}\)

Ta có : \(4a^2+b^2=5ab\)
\(\Rightarrow4a^2-4ab+b^2=ab\)
\(\Rightarrow\left(2a-b\right)^2=ab\)
Vì \(0< b< 2a\)\(\Rightarrow2a-b>0\)
\(\Rightarrow2a-b=ab\)
\(\Rightarrow M=\frac{ab}{4a^2-b^2}=\frac{2a-b}{\left(2a-b\right)\left(2a+b\right)}=\frac{1}{2a+b}\)
Vậy \(M=\frac{1}{2a+b}\)

Ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}=\frac{-1}{c}\)
\(\Leftrightarrow\left(\frac{1}{a}+\frac{1}{b}\right)^3=\left(-\frac{1}{c}\right)^3\)
\(\Leftrightarrow\frac{1}{a^3}+\frac{1}{b^3}+\frac{3}{ab}\left(\frac{1}{a}+\frac{1}{b}\right)=-\frac{1}{c^3}\)
\(\Leftrightarrow\frac{1}{a^3}+\frac{1}{b^3}-\frac{3}{abc}=-\frac{1}{c^3}\)
\(\Leftrightarrow\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
Lại có: \(N=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=abc\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)=abc.\frac{3}{abc}=3\)

\(P=\frac{a-b}{a+b}\) \(\Leftrightarrow P^2=\left(\frac{a-b}{a+b}\right)^2=\frac{a^2+b^2-2ab}{a^2+b^2+2ab}=\frac{3a^2+3b^2-6ab}{3a^2+3b^2+6ab}=\frac{10ab-6ab}{10ab+6ab}=\frac{4ab}{16ab}=\frac{1}{4}\)
Vì 0 < a < b => a - b < 0, a + b > 0 \(\Rightarrow P=\frac{a-b}{a+b}< 0\)
\(\Rightarrow P=\frac{1}{2}\)


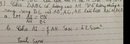
9x2 + 4y2 = 20xy
=> 9x2 - 20xy + 4y2 = 0
=> 9x2 - 18xy - 2xy + 4y2 = 0
=> 9x(x - 2y) - 2y(x - 2y) = 0
=> (9x - 2y)(x - 2y) = 0
=> \(\orbr{\begin{cases}9x=2y\\x=2y\end{cases}}\)
Khi x = 2y
=> 2y.3x = x.3x = 3x2 \(\ge\)0 (loại)
Khi 9x = 2y
=> 2y.3x = 9x.3x = 27x2 \(\ge0\)(loại)
Vậy không tính được B sao cho thỏa mãn đề bài